题目内容
已知x、y∈R,2y2-x2=1,则x2+4y2-4xy的最小值为_____________.
解法一:∵2xy≤x2+y2,∴x2+4y2-4xy≥x2+4y2-2(x2+y2)=2y2-x2=1.
当且仅当x=y时取等号.
解法二:x2+4y2-4xy=(x-2y)2.
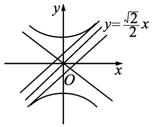
令t=|x-2y|,则问题转化为求t=|x-2y|的最小值.而2y2-x2=1表示实轴在y轴上的双曲线.
当x-2y≥0时,t=x-2y,即直线x-2y-t=0与下支相切时,t最小;
当x-2y≤0时,t=2y-x,即直线x-2y+t=0与上支相切时,t最小.
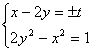
![]() 2·
2·![]() -x2=1,
-x2=1,
x2±2tx+2-t2=0,
Δ=4t2-4(2-t2)=0.
∴t2=1.∴t=1或t=-1.
∴x2+4y2-4xy的最小值为1.
答案:1

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目