题目内容
已知函数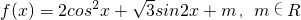
(1)当x∈R时,求f(x)的单调递增区间;
(2)当 时,且f(x)的最小值为2,求m的值.
时,且f(x)的最小值为2,求m的值.
解:(1)由题意可得:

=
= ,
,
由正弦函数的单调性可得: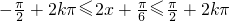 ,k∈z
,k∈z
即得到: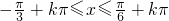 ,
,
∴f(x)的单调递增区间为 ,k∈Z
,k∈Z
(2)∵
∴
∴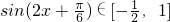
∴f(x)的最小值为m
∴m=2.
分析:(1)由题意可得:f(x)= ,由正弦函数的单调性可得:
,由正弦函数的单调性可得: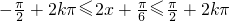 ,k∈z
,k∈z
进而得到f(x)的单调递增区间.
(2)因为 ,所以
,所以 ,所以
,所以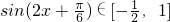 ,即可求出m的数值.
,即可求出m的数值.
点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,以及熟练掌握利用整体思想解决数学问题的方法.

=

=
 ,
,由正弦函数的单调性可得:
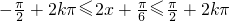 ,k∈z
,k∈z即得到:
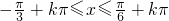 ,
,∴f(x)的单调递增区间为
 ,k∈Z
,k∈Z(2)∵

∴

∴
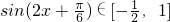
∴f(x)的最小值为m
∴m=2.
分析:(1)由题意可得:f(x)=
 ,由正弦函数的单调性可得:
,由正弦函数的单调性可得: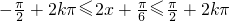 ,k∈z
,k∈z进而得到f(x)的单调递增区间.
(2)因为
 ,所以
,所以 ,所以
,所以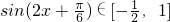 ,即可求出m的数值.
,即可求出m的数值.点评:解决此类问题的关键是熟练掌握正弦函数的有关性质,以及熟练掌握利用整体思想解决数学问题的方法.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目

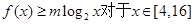 恒成立,求m的取值范围
恒成立,求m的取值范围
 恒成立,求m的取值范围.
恒成立,求m的取值范围.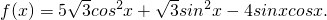
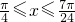 ,求f(x)的单调区间.
,求f(x)的单调区间.
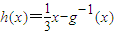 在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
 ,求f(x)的单调区间.
,求f(x)的单调区间.