题目内容
设ω＞0，若函数f（x）=2sinωx在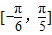
上单调递增，则ω的取值范围是（ ）A．
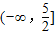
B．
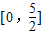
C．
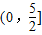
D．
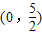
【答案】分析：由三角函数的增区间的公式，算出f（x）距离原点最近的单调增区间为[-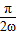
，
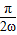]，由此结合题意建立关于ω的不等式，解之可得ω的取值范围．
解答：解：∵函数f（x）=2sinωx的单调增区间满足-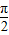
+2kπ≤ωx≤
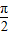+2kπ，（k∈Z）
∴取k=0，得到距离原点最近的单调增区间为[-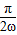
，
]
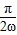∵在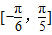
上f（x）单调递增
∴-
≥-
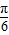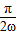且
≥
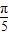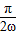，解之得0＜ω≤
故选：C
点评：本题给出三角函数式，在已知函数的增区间情况下求参数的取值范围．着重考查了三角函数的单调区间公式和不等式的解法等知识，属于中档题．
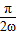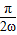，]，由此结合题意建立关于ω的不等式，解之可得ω的取值范围．解答：解：∵函数f（x）=2sinωx的单调增区间满足-
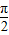+2kπ≤ωx≤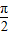+2kπ，（k∈Z）∴取k=0，得到距离原点最近的单调增区间为[-
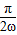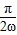，]∵在
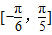上f（x）单调递增∴-
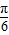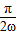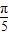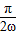≥-且≥，解之得0＜ω≤故选：C
点评：本题给出三角函数式，在已知函数的增区间情况下求参数的取值范围．着重考查了三角函数的单调区间公式和不等式的解法等知识，属于中档题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目