题目内容

【题目】设椭圆 的左、右焦点分别为F1 ， F2 ， 离心率为e，过F2的直线与椭圆的交于A，B两点，若△F1AB是以A为顶点的等腰直角三角形，则e2=（ ）
A.3﹣2
B.5﹣3
C.9﹣6
D.6﹣4

【答案】D
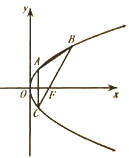
【解析】解：解：如图，设|F1F2|=2c，|AF1|=m，
若△ABF1构成以A为直角顶点的等腰直角三角形，
则|AB|=|AF1|=m，|BF1|= m，
由椭圆的定义可得△ABF1的周长为4a，
即有4a=2m+ m，即m=2（2﹣ ）a，
则|AF2|=2a﹣m=（2 ﹣2）a，
在直角三角形AF1F2中，
|F1F2|2=|AF1|2+|AF2|2 ， 即4c2=4（2﹣ ）2a2+4（ ﹣1）2a2 ，
∴c2=（9﹣6 ）a2 ， 则e2= =9﹣6 ．
故选：D．

练习册系列答案
相关题目

【题目】已知x，y满足约束条件 ，若z=ax+y的最大值为4，则a=（ ）
A.3
B.2
C.﹣2
D.﹣3

【题目】已知函数f（x）=x﹣ ． （Ⅰ）判断f（x）的奇偶性；
（Ⅱ）用函数单调性的定义证明：f（x）在（0，+∞）上是增函数．

【题目】已知点A（﹣2，0），B（2，0），P（x0 ， y0）是直线y=x+3上任意一点，以A，B为焦点的椭圆过P，记椭圆离心率e关于x0的函数为e（x0），那么下列结论正确的是（ ）
A.e与x0一一对应
B.函数e（x0）无最小值，有最大值
C.函数e（x0）是增函数
D.函数e（x0）有最小值，无最大值

【题目】如图所示，在矩形ABCD中，AD=2，AB=1，点E是AD的中点，将△DEC沿CE折起到△D′EC的位置，使二面角D′﹣EC﹣B是直二面角．

（1）证明：BE⊥CD′；
（2）求二面角D′﹣BC﹣E的余弦值．

【题目】如图所示几何体的三视图，则该几何体的表面积为 ．

【题目】如图，已知F为抛物线y2=4x的焦点，点A，B，C在该抛物线上，其中A，C关于x轴对称（A在第一象限），且直线BC经过点F．

（1）若△ABC的重心为G（ ），求直线AB的方程；
（2）设S△ABO=S1 ， S△CFO=S2 ， 其中O为坐标原点，求S12+S22的最小值．

【题目】已知函数f（x）= ax2﹣（2a+1）x+2lnx（a∈R）． （Ⅰ）若曲线y=f（x）在x=1和x=3处的切线互相平行，求a的值；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=x2﹣2x，若对任意x1∈（0，2]，均存在x2∈（0，2]，使得f（x1）＜g（x2），求a的取值范围．

【题目】已知α是第二象限角，且cos（α+π）= ．
（1）求tanα的值；
（2）求sin（α﹣ ）sin（﹣α﹣π）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网