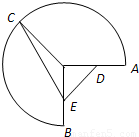
题目内容
如图,半径为1圆心角为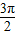 圆弧
圆弧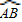 上有一点C.
上有一点C.(1)当C为圆弧
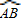 中点时,D为线段OA上任一点,求
中点时,D为线段OA上任一点,求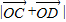 的最小值.
的最小值.(2)当C在圆弧
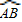 上运动时,D、E分别为线段OA、OB的中点,求
上运动时,D、E分别为线段OA、OB的中点,求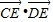 的取值范围.
的取值范围.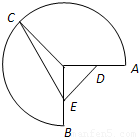
【答案】分析:(1)以O为原点,以 为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),求出C坐标,推出
为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),求出C坐标,推出 ,求出
,求出 的表达式,然后求出模的最小值.
的表达式,然后求出模的最小值.
(2)设 =(cosα,sinα)(0≤α≤
=(cosα,sinα)(0≤α≤ π),求出
π),求出 的表达式结合
的表达式结合 ≤
≤ ≤
≤ ,求出
,求出 的取值范围.
的取值范围.
解答: 解:(1)以O为原点,以
解:(1)以O为原点,以 为x轴正方向,建立图示坐标系,
为x轴正方向,建立图示坐标系,
设D(t,0)(0≤t≤1),C( )…2′
)…2′
∴ =(
=( )
)
∴ =
= =
= (0≤t≤1)…4′
(0≤t≤1)…4′
当 时,最小值为
时,最小值为 …6′
…6′
(2)设 =(cosα,sinα)(0≤α≤
=(cosα,sinα)(0≤α≤ π)
π)
 =(0,
=(0, )-(cosα,sinα)
)-(cosα,sinα)
=( )…8′
)…8′
又∵D( ),E(0,
),E(0, )
)
∴ =(
=( )…10′
)…10′
∴ =
= =
= …12′
…12′
∵ ≤
≤ ≤
≤ …13′
…13′
∴ ∈[
∈[ ]…14′
]…14′
点评:本题考查向量的数量积,向量的表示方法,三角运算,考查转化思想,计算能力.
 为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),求出C坐标,推出
为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),求出C坐标,推出 ,求出
,求出 的表达式,然后求出模的最小值.
的表达式,然后求出模的最小值.(2)设
 =(cosα,sinα)(0≤α≤
=(cosα,sinα)(0≤α≤ π),求出
π),求出 的表达式结合
的表达式结合 ≤
≤ ≤
≤ ,求出
,求出 的取值范围.
的取值范围.解答:
 解:(1)以O为原点,以
解:(1)以O为原点,以 为x轴正方向,建立图示坐标系,
为x轴正方向,建立图示坐标系,设D(t,0)(0≤t≤1),C(
 )…2′
)…2′∴
 =(
=( )
)∴
 =
= =
= (0≤t≤1)…4′
(0≤t≤1)…4′当
 时,最小值为
时,最小值为 …6′
…6′(2)设
 =(cosα,sinα)(0≤α≤
=(cosα,sinα)(0≤α≤ π)
π) =(0,
=(0, )-(cosα,sinα)
)-(cosα,sinα)=(
 )…8′
)…8′又∵D(
 ),E(0,
),E(0, )
)∴
 =(
=( )…10′
)…10′∴
 =
= =
= …12′
…12′∵
 ≤
≤ ≤
≤ …13′
…13′∴
 ∈[
∈[ ]…14′
]…14′点评:本题考查向量的数量积,向量的表示方法,三角运算,考查转化思想,计算能力.

练习册系列答案
相关题目
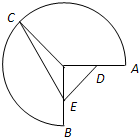 如图,半径为1圆心角为
如图,半径为1圆心角为
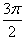 圆弧
圆弧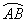 上有一点C,
上有一点C,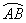 中点时,D为线段OA上任一点,求
中点时,D为线段OA上任一点,求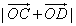 的最小值;
的最小值;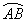 上运动时,D、E分别为线段OA、OB的中点,求
上运动时,D、E分别为线段OA、OB的中点,求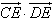 的取值范围。
的取值范围。 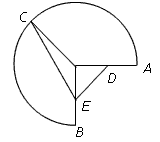
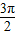 圆弧
圆弧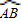 上有一点C.
上有一点C.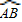 中点时,D为线段OA上任一点,求
中点时,D为线段OA上任一点,求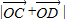 的最小值.
的最小值.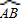 上运动时,D、E分别为线段OA、OB的中点,求
上运动时,D、E分别为线段OA、OB的中点,求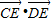 的取值范围.
的取值范围.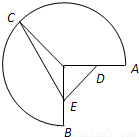
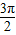 圆弧
圆弧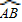 上有一点C.
上有一点C.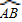 中点时,D为线段OA上任一点,求
中点时,D为线段OA上任一点,求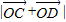 的最小值.
的最小值.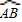 上运动时,D、E分别为线段OA、OB的中点,求
上运动时,D、E分别为线段OA、OB的中点,求 的取值范围.
的取值范围.