题目内容
1．已知a，b∈R，函数f（x）=-$\frac{1}{3}{x}^{3}+\frac{a}{2}{x}^{2}+bx$有两个极值点x1，x2（x1＜x2），f（x2）=x2，则方程f2（x）-af（x）-b=0的实根个数（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 0 |
分析 由函数f（x）=-$\frac{1}{3}{x}^{3}+\frac{a}{2}{x}^{2}+bx$有两个极值点x1，x2，可得x2-ax-b=0有两个不相等的根，必有△=a2+4b＞0．而方程f2（x）-af（x）-b=0的△1=△＞0，可知此方程有两解且f（x）=x1或x2．再分别讨论利用平移变换即可解出方程f（x）=x1或f（x）=x2解的个数．
解答 解：∵f（x）=-$\frac{1}{3}{x}^{3}+\frac{a}{2}{x}^{2}+bx$，
∴f′（x）=-x2+ax+b，
由题意知x1，x2是函数的两个极值点，
∴x2-ax-b=0有两个不相等的根，
∴△=a2+4b＞0．
∵x1＜x2，
∴x1=$\frac{a-\sqrt{{a}^{2}+4b}}{2}$，x2=$\frac{a+\sqrt{{a}^{2}+4b}}{2}$．
而方程f2（x）-af（x）-b=0的△1=△＞0，
∴此方程有两解且f（x）=x1或x2
即有0＜x1＜x2，f（x2）＞0．
①把y=f（x）向下平移x2个单位即可得到y=f（x）-x2的图象，
∵f（x2）=x2，可知方程f（x）=x2有两解．
②把y=f（x）向下平移x1个单位即可得到y=f（x）-x1的图象，
∵f（x2）=x2，∴f（x2）-x1＞0，可知方程f（x）=x1只有一解．
综上①②可知：方程f（x）=x1或f（x）=x2只有3个实数解．
即关于x的方程f2（x）-af（x）-b=0的只有3不同实根．
故选：B．
点评 本题综合考查了利用导数研究函数得单调性、极值及方程解得个数、平移变换等基础知识，考查了图象平移的思想方法、推理能力、计算能力、分析问题和解决问题的能力．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
的图象向左平移
个单位长度，所得图象对应的函数（ ）
上单调递减 B．在区间
上单调递减 D．在区间
9．已知函数f（x）=sin（ωx+$\frac{π}{3}$）+$\sqrt{3}$sin（ωx-$\frac{π}{6}$）（ω＞0，x∈R）的最小正周期为π，则（ ）
| A． | f（x）为偶函数 | B． | f（x）在[-$\frac{π}{2}$，$\frac{π}{2}$]上单调递增 | ||
| C． | x=$\frac{π}{2}$为f（x）的图象的一条对称轴 | D． | （$\frac{π}{2}$，0）为f（x）的图象的一个对称中心 |
6．若x，y满足$\left\{\begin{array}{l}x+y≥0\\ x≥1\\ x-y≥0\end{array}\right.$，则下列不等式恒成立的是（ ）
| A． | y≥-1 | B． | x≥2 | C． | x+2y+2≥0 | D． | 2x-y+1≥0 |
12．已知不共线向量$\overrightarrow{a}$，$\overrightarrow{b}$，|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
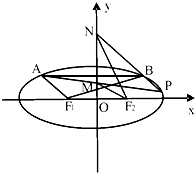如图，F1，F2分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，且焦距为2$\sqrt{2}$，动弦AB平行于x轴，且|F1A|+|F2A|=4．