题目内容
已知函数 ,则该函数的值域为
,则该函数的值域为
- A.[-1,1]
- B.[-2,2]
- C.(-∞,-2]∪[2,+∞)
- D.(-∞,-1]∪[1,+∞)
C
分析:设 sinx=t,t∈[-1,1],且t≠0,利用单调性求出当 0<t≤1时,y≥2,同理求得-1≤t<0 时,y≤-2,从而求得函数y的值域.
解答:函数 =sinx+
=sinx+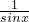 ,设 sinx=t,t∈[-1,1],且t≠0,
,设 sinx=t,t∈[-1,1],且t≠0,
则 y=t+ ,t∈[-1,1],且t≠0,故函数y为奇函数.
,t∈[-1,1],且t≠0,故函数y为奇函数.
当 0<t≤1时,函数y为单调减函数,故 t=1时,函数y取得最小值等于2,此时,y≥2.
根据奇函数 的性质可得,-1≤t<0 时,y≤-2,故函数y的值域为 (-∞,-2]∪[2,+∞),
故选C.
点评:本题考查正弦函数的值域,函数y=t+ ,t∈[-1,1]且t≠0 的单调性和值域的求法,求得当0<t≤1时,y≥2,是解题的关键.
,t∈[-1,1]且t≠0 的单调性和值域的求法,求得当0<t≤1时,y≥2,是解题的关键.
分析:设 sinx=t,t∈[-1,1],且t≠0,利用单调性求出当 0<t≤1时,y≥2,同理求得-1≤t<0 时,y≤-2,从而求得函数y的值域.
解答:函数
 =sinx+
=sinx+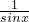 ,设 sinx=t,t∈[-1,1],且t≠0,
,设 sinx=t,t∈[-1,1],且t≠0,则 y=t+
 ,t∈[-1,1],且t≠0,故函数y为奇函数.
,t∈[-1,1],且t≠0,故函数y为奇函数.当 0<t≤1时,函数y为单调减函数,故 t=1时,函数y取得最小值等于2,此时,y≥2.
根据奇函数 的性质可得,-1≤t<0 时,y≤-2,故函数y的值域为 (-∞,-2]∪[2,+∞),
故选C.
点评:本题考查正弦函数的值域,函数y=t+
 ,t∈[-1,1]且t≠0 的单调性和值域的求法,求得当0<t≤1时,y≥2,是解题的关键.
,t∈[-1,1]且t≠0 的单调性和值域的求法,求得当0<t≤1时,y≥2,是解题的关键. 
练习册系列答案
相关题目
 ,则该函数的值域为__________.
,则该函数的值域为__________. ,则该函数的定义域为( )
,则该函数的定义域为( ) B.
B. C.
C. D.
D. 
 ,则该函数的定义域为(
)
,则该函数的定义域为(
) B.
R C.
B.
R C.  D.
D.

 ,则该函数的值域为( )
,则该函数的值域为( ) ,则该函数的图象( )
,则该函数的图象( ) 对称
对称 对称
对称 对称
对称 对称
对称