Question

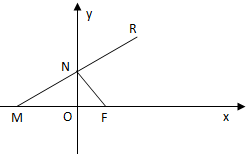（2006•嘉定区二模）如图，已知点F（1，0），点M在x轴上，点N在y轴上，且

NM

•

NF

=0，点R满足

NM

+

NR

=

0

．
（1）求动点R的轨迹C的方程；
（2）过B（4，0）作直线l交轨迹C于P、Q两点，求

OP

•

OQ

的值．

Answer 1

分析：（1）由已知，N是MR的中点，设R（x，y），则M（-x，0），N(0，

y

2

)，由

NM

•

NF

=0可得x，y的方程；
（2）分两种情况进行讨论：①若直线l垂直于轴，易求；②当直线l不垂直于x轴时，设l的方程为y=k（x-4），与抛物线方程联立方程组并消掉x可得y的二次方程，设P（x₁，y₁），Q（x₂，y₂），
由韦达定理及数量积运算可求得结果；

解答：解：（1）由已知，N是MR的中点，设R（x，y），则M（-x，0），N(0，

y

2

)，
∴

NM

={-x，-

y

2

}，

NF

={1，-

y

2

}，
由

NM

•

NF

=0，得-x+

y2

4

=0，即y²=4x，
∴动点R的轨迹方程为y²=4x；
（2）①若直线l垂直于轴，则的方程为x=4，则P（4，4），Q（4，-4），

OP

•

OQ

=0；
②当直线l不垂直于x轴时，设l的方程为y=k（x-4），
由

y=k(x-4) y2=4x

，得ky²-4y-16k=0，
当k≠0时，直线l与抛物线总有两个交点．
设P（x₁，y₁），Q（x₂，y₂），则y1+y2=

4

k

，y₁y₂=-16，
∴

OP

•

OQ

=x1x2+y1y2=

(y1y2)2

16

+y1y2=16-16=0，
综上，

OP

•

OQ

=0；

点评：本题考查平面向量数量积的运算、向量与圆锥曲线的综合，考查学生分析解决问题的能力．