题目内容
对于x∈(1,2],关于x的不等式 <1总成立,求实数a的取值范围.
<1总成立,求实数a的取值范围.
解:由1<x≤2,得a>0,a+x>1,
∴lg(a+x)>0
∵ <1总成立
<1总成立
∴lg2ax<lg(a+x),即2ax<a+x
∴(2a-1)x<a总成立
(1)a> 时,x<
时,x< ,由1<x≤2时x<
,由1<x≤2时x< 总成立,得
总成立,得 >2,
>2,
∴ <a<
<a<
(2)a= 时,有0•x<
时,有0•x<
∴1<x≤2时不等式总成立
(3)0<a< 时,x>
时,x> ,由1<x≤2时x>
,由1<x≤2时x> 总成立,
总成立,
∴a≤1,
综合0<a< ,得0<a<
,得0<a<
综上三类讨论可得,0<a<
分析:由题意可得,lg(a+x)>0,则由不等式 <1总成立可得(2a-1)x<a总成立,从而需要对2a-1的正负讨论
<1总成立可得(2a-1)x<a总成立,从而需要对2a-1的正负讨论
(1)a> 时,由1<x≤2时x<
时,由1<x≤2时x< 可得x<
可得x< 的最小值即可;(2)a=
的最小值即可;(2)a= 时,(3)0<a<
时,(3)0<a< 时,x>
时,x> ,x>
,x> 的最大值即可,从而可求a的范围
的最大值即可,从而可求a的范围
点评:本题主要考查了对数函数的单调性在不等式中的应用,函数的恒成立与函数最值求解的相互转化,要注意分类讨论思想的应用.
∴lg(a+x)>0
∵
 <1总成立
<1总成立∴lg2ax<lg(a+x),即2ax<a+x
∴(2a-1)x<a总成立
(1)a>
 时,x<
时,x< ,由1<x≤2时x<
,由1<x≤2时x< 总成立,得
总成立,得 >2,
>2,∴
 <a<
<a<
(2)a=
 时,有0•x<
时,有0•x<
∴1<x≤2时不等式总成立
(3)0<a<
 时,x>
时,x> ,由1<x≤2时x>
,由1<x≤2时x> 总成立,
总成立,∴a≤1,
综合0<a<
 ,得0<a<
,得0<a<
综上三类讨论可得,0<a<

分析:由题意可得,lg(a+x)>0,则由不等式
 <1总成立可得(2a-1)x<a总成立,从而需要对2a-1的正负讨论
<1总成立可得(2a-1)x<a总成立,从而需要对2a-1的正负讨论(1)a>
 时,由1<x≤2时x<
时,由1<x≤2时x< 可得x<
可得x< 的最小值即可;(2)a=
的最小值即可;(2)a= 时,(3)0<a<
时,(3)0<a< 时,x>
时,x> ,x>
,x> 的最大值即可,从而可求a的范围
的最大值即可,从而可求a的范围点评:本题主要考查了对数函数的单调性在不等式中的应用,函数的恒成立与函数最值求解的相互转化,要注意分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.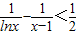 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立. <1总成立,求实数a的取值范围.
<1总成立,求实数a的取值范围.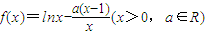 .
.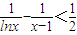 对于x∈(1,2)恒成立.
对于x∈(1,2)恒成立.