题目内容
设集合A={x|x2+3k2≥2k(2x-1)},B={x|x2-(2x-1)k+k2≥0},且A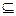 B,试求k的取值范围.
B,试求k的取值范围.
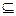 B,试求k的取值范围.
B,试求k的取值范围.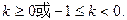
解: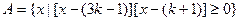 ,比较
,比较
因为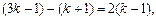
(1)当k>1时,3k-1>k+1,A={x|x≥3k-1或x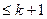 }.
}.
(2)当k=1时,x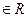 .
.
(3)当k<1时,3k-1<k+1,A=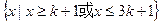 .
.
B中的不等式不能分解因式,故考虑判断式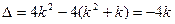 ,
,
(1)当k=0时,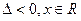 .
.
(2)当k>0时,△<0,x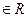 .
.
(3)当k<0时,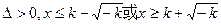 .
.
故:当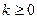 时,由B=R,显然有A
时,由B=R,显然有A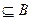 ,
,
当k<0时,为使A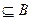 ,需要
,需要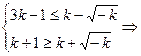 k
k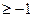 ,于是k
,于是k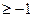 时,
时,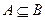 .
.
综上所述,k的取值范围是: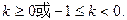
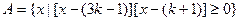 ,比较
,比较
因为
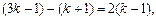
(1)当k>1时,3k-1>k+1,A={x|x≥3k-1或x
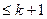 }.
}.(2)当k=1时,x
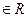 .
.(3)当k<1时,3k-1<k+1,A=
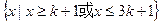 .
.B中的不等式不能分解因式,故考虑判断式
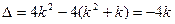 ,
,(1)当k=0时,
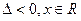 .
.(2)当k>0时,△<0,x
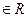 .
.(3)当k<0时,
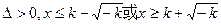 .
.故:当
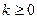 时,由B=R,显然有A
时,由B=R,显然有A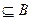 ,
,当k<0时,为使A
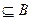 ,需要
,需要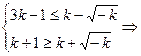 k
k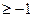 ,于是k
,于是k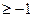 时,
时,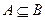 .
.综上所述,k的取值范围是:

练习册系列答案
相关题目
 bn=
bn=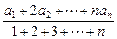 ,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
,求证:数列{an}成等差数列的充要条件是数列{bn}也是等差数列。
 ,使得对于
,使得对于 ,都有
,都有 (
( ),则称
),则称 是M的最大(小)值.若A是一个不含零的非空实数集,且
是M的最大(小)值.若A是一个不含零的非空实数集,且 是A的最大值,则( )
是A的最大值,则( ) 时,
时, 是集合
是集合 的最小值
的最小值 时,
时, 的最小值
的最小值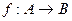 ,其中
,其中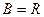 ,对法则:
,对法则: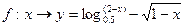 对于实数
对于实数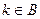 ,在集合A中不存在原象,则
,在集合A中不存在原象,则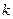 的取值范围是 ( )
的取值范围是 ( )
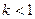


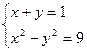 的解集是( )
的解集是( )


 。
。 ,
,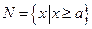 ,且
,且 ,则实数a的取值范围是
,则实数a的取值范围是

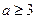

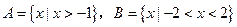 ,则
,则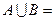 ( )
( )


