题目内容
设f(x)是R上的偶函数,且在[0,+∞)上单调递增,若a<b<0,则
- A.f(a)<f(b)
- B.f(a)>f(b)
- C.f(a)=f(b)
- D.无法确定
B
分析:根据偶函数对称区间上的单调性相反可知f(x)在(-∞,0)上单调递减,从而可比较函数值的大小
解答:∵f(x)是R上的偶函数,且在[0,+∞)上单调递增
∴f(x)在(-∞,0)上单调递减
∵a<b<0,
∴f(a)>f(b)
故选B
点评:本题主要考查了利用函数的奇偶性比较函数值的大小,解题的关键是偶函数的对称区间上的单调性相反性质的应用
分析:根据偶函数对称区间上的单调性相反可知f(x)在(-∞,0)上单调递减,从而可比较函数值的大小
解答:∵f(x)是R上的偶函数,且在[0,+∞)上单调递增
∴f(x)在(-∞,0)上单调递减
∵a<b<0,
∴f(a)>f(b)
故选B
点评:本题主要考查了利用函数的奇偶性比较函数值的大小,解题的关键是偶函数的对称区间上的单调性相反性质的应用

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
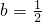 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由. ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.