题目内容
已知双曲线方程为
，其中正数a、b的等差中项是
，一个等比中项是
，且a＞b，则双曲线的离心率为
- A.
- B.
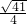
- C.
- D.
D
分析：根据正数a、b的等差中项是，一个等比中项是，可得a与b并且根据c=
求出c，进而求出双曲线的离心率．
解答：由题意可得：
，解得a=5，b=4，
∴c2=a2+b2=（a+b）2-2ab=41，
所以c=
，
所以离心率e=．
故选D．
点评：本题主要考查了双曲线的简单性质．
分析：根据正数a、b的等差中项是
，一个等比中项是，可得a与b并且根据c=求出c，进而求出双曲线的离心率．解答：由题意可得：
，解得a=5，b=4，∴c2=a2+b2=（a+b）2-2ab=41，
所以c=
，所以离心率e=
．故选D．
点评：本题主要考查了双曲线的简单性质．
练习册系列答案
相关题目
，以定点
为中点的弦存在吗？若存在，求出其所在直线的方程，若不存在，请说明理由．
，
的顶点是该双曲线的中心，而焦点是其左顶点，求抛物线
经过点
，其渐近线方程为y=±2x，