题目内容
已知等差数列 满足:
满足: .
.
(Ⅰ)求 的通项公式及前
的通项公式及前 项和
项和 ;
;
(Ⅱ)若等比数列 的前
的前 项和为
项和为 ,且
,且 ,求
,求 .
.
【答案】
(I) ; (II)
; (II) .
.
【解析】
试题分析:(Ⅰ)设等差数列 的公差为
的公差为 ,由
,由 得两个含首项
得两个含首项 和公差
和公差 的方程,解这个方程组求得
的方程,解这个方程组求得 和
和 ,即可得通项公式,再利用等差数列的求和公式即可得前
,即可得通项公式,再利用等差数列的求和公式即可得前 项和
项和 .
.
(Ⅱ)设等比数列 的公比为
的公比为 ,由(Ⅰ)和题设得:
,由(Ⅰ)和题设得: ,
,  ,再用等比数列的通项公式即可求得公比,然后用等比数列的求和公式即可求得前
,再用等比数列的通项公式即可求得公比,然后用等比数列的求和公式即可求得前 项和
项和 .
.
试题解析:(Ⅰ)设等差数列 的公差为
的公差为 ,由题设得:
,由题设得:
 , (2分)
, (2分)
即 ,解得
,解得 . (4分)
. (4分)
 , (5分)
, (5分)
 . (7分)
. (7分)
(Ⅱ)设等比数列 的公比为
的公比为 ,由(Ⅰ)和题设得:
,由(Ⅰ)和题设得:
 ,
,  . (9分)
. (9分)
 , (10分)
, (10分)
 . (11分)
. (11分)
 数列
数列 是以
是以 为首项,公比
为首项,公比 的等比数列.
的等比数列.
 . (13分)
. (13分)
考点:等差数列与等比数列.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 满足
满足 ,
, ,
, ,则
,则 的值为 .
的值为 . 满足:
满足: ,
, ,该数列的前三项分别加上
,该数列的前三项分别加上 ,
, 后顺次成为等比数列
后顺次成为等比数列 的前三项. 求数列
的前三项. 求数列 =____________
=____________ 满足,
满足,
 。(1)求
。(1)求 和
和
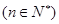 ,求数列
,求数列 的前n项和
的前n项和
 满足
满足 ,
, ,
,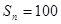 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.