题目内容
已知向量 =(cos
=(cos ,-1),
,-1), =(
=( sin
sin ,cos2
,cos2 ),设函数f(x)=
),设函数f(x)= +
+ .
.
(1)若x∈[0, ],f(x)=
],f(x)= ,求cosx的值;
,求cosx的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c- a,求f(B)的取值范围.
a,求f(B)的取值范围.
解:(1)依题意得f(x)= +
+ =
= sin
sin  cos
cos -cos2
-cos2 +
+ =
= sinx-
sinx-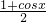 +
+ =sin(x-
=sin(x- ),…(2分)
),…(2分)
由 x∈[0, ],得:-
],得:- ≤x-
≤x- ≤
≤ ,sin(x-
,sin(x- )=
)= >0,
>0,
从而可得 cos(x- )=
)= ,…(4分)
,…(4分)
则cosx=cos[(x- )+
)+ ]=cos(x-
]=cos(x- ) sin
) sin -sin(x-
-sin(x- ) cos
) cos =
=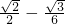 . …(6分)
. …(6分)
(2)在△ABC中,由2bcosA≤2c- a 得 2sinBcosA≤2sin(A+B)-
a 得 2sinBcosA≤2sin(A+B)- sinA,即 2sinAcosB≥
sinA,即 2sinAcosB≥ sinA,
sinA,
由于sinA>0,故有cosB≥ ,从而 0<B≤
,从而 0<B≤ ,…(10分)
,…(10分)
故f(B)=sin(B- ),由于 0<B≤
),由于 0<B≤ ,∴-
,∴- <B-
<B- ≤0,∴sin(B-
≤0,∴sin(B- )∈(-
)∈(- ,0],即f(B)∈(-
,0],即f(B)∈(- ,0]. …(12分)
,0]. …(12分)
分析:(1)依题意得f(x)= +
+ =sin(x-
=sin(x- )=
)= ,由 x∈[0,
,由 x∈[0, ],sin(x-
],sin(x- )=
)= >0,cos(x-
>0,cos(x- )=
)= ,由cosx=cos[(x-
,由cosx=cos[(x- )+
)+ ]利用两角和的余弦公式求得结果.
]利用两角和的余弦公式求得结果.
(2)由2bcosA≤2c- a 得:cosB≥
a 得:cosB≥ ,从而 0<B≤
,从而 0<B≤ ,由此求得f(B)=sin(B-
,由此求得f(B)=sin(B- )的取值范围.
)的取值范围.
点评:本题主要考查三角函数的恒等变换及化简求值,两角和的余弦公式,两个向量的数量积公式的应用,属于中档题.
 +
+ =
= sin
sin  cos
cos -cos2
-cos2 +
+ =
= sinx-
sinx-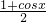 +
+ =sin(x-
=sin(x- ),…(2分)
),…(2分)由 x∈[0,
 ],得:-
],得:- ≤x-
≤x- ≤
≤ ,sin(x-
,sin(x- )=
)= >0,
>0,从而可得 cos(x-
 )=
)= ,…(4分)
,…(4分)则cosx=cos[(x-
 )+
)+ ]=cos(x-
]=cos(x- ) sin
) sin -sin(x-
-sin(x- ) cos
) cos =
=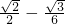 . …(6分)
. …(6分)(2)在△ABC中,由2bcosA≤2c-
 a 得 2sinBcosA≤2sin(A+B)-
a 得 2sinBcosA≤2sin(A+B)- sinA,即 2sinAcosB≥
sinA,即 2sinAcosB≥ sinA,
sinA,由于sinA>0,故有cosB≥
 ,从而 0<B≤
,从而 0<B≤ ,…(10分)
,…(10分)故f(B)=sin(B-
 ),由于 0<B≤
),由于 0<B≤ ,∴-
,∴- <B-
<B- ≤0,∴sin(B-
≤0,∴sin(B- )∈(-
)∈(- ,0],即f(B)∈(-
,0],即f(B)∈(- ,0]. …(12分)
,0]. …(12分)分析:(1)依题意得f(x)=
 +
+ =sin(x-
=sin(x- )=
)= ,由 x∈[0,
,由 x∈[0, ],sin(x-
],sin(x- )=
)= >0,cos(x-
>0,cos(x- )=
)= ,由cosx=cos[(x-
,由cosx=cos[(x- )+
)+ ]利用两角和的余弦公式求得结果.
]利用两角和的余弦公式求得结果.(2)由2bcosA≤2c-
 a 得:cosB≥
a 得:cosB≥ ,从而 0<B≤
,从而 0<B≤ ,由此求得f(B)=sin(B-
,由此求得f(B)=sin(B- )的取值范围.
)的取值范围.点评:本题主要考查三角函数的恒等变换及化简求值,两角和的余弦公式,两个向量的数量积公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |