题目内容
11.已知向量$\overrightarrow a=(2,1),\overrightarrow b=(x,-1)$,且$\overrightarrow a-\overrightarrow b$与$\overrightarrow b$共线,则x的值为-2.分析 根据平面向量的坐标运算以及两向量共线的坐标表示,列出方程求出x的值.
解答 解:∵向量$\overrightarrow a=(2,1),\overrightarrow b=(x,-1)$,
∴$\overrightarrow{a}$-$\overrightarrow{b}$=(2-x,2),
又$\overrightarrow a-\overrightarrow b$与$\overrightarrow b$共线,
∴(2-x)×(-1)-2x=0,
解得x=-2.
故答案为:-2.
点评 本题考查了平面向量的坐标运算问题,是基础题目.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
19.在△ABC中,若a=6,b=9,A=45°,则此三角形有( )
| A. | 一解 | B. | 两解 | C. | 无解 | D. | 解的个数不确定 |
6.投掷两枚骰子,则点数之和是8的概率为( )
| A. | $\frac{5}{36}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{12}$ |
3.在空间四边形OABC中,M为BC的中点,N为OM的中点,连接AC,则向量$\overrightarrow{AO}+\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)化简后的结果为( )
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.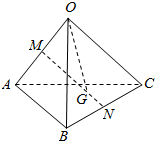 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.