题目内容
已知函数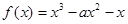 ;
;
(1)若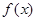 在
在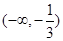 上单调递增,在
上单调递增,在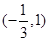 上单调递减,在
上单调递减,在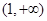 上单调递增,求实数
上单调递增,求实数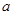 的值;
的值;
(2)当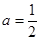 时,求证:当
时,求证:当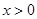 时,
时,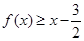 .
.
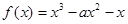 ;
;(1)若
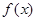 在
在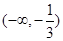 上单调递增,在
上单调递增,在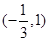 上单调递减,在
上单调递减,在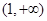 上单调递增,求实数
上单调递增,求实数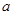 的值;
的值;(2)当
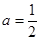 时,求证:当
时,求证:当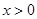 时,
时,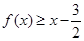 .
.(1)  ;(2)分析法。
;(2)分析法。
 ;(2)分析法。
;(2)分析法。试题分析:


 ,要证
,要证 ,即证
,即证 ,
,令
 ,
, 
 ,
, ,
,  在
在 ,
, 

点评:中档题,本题属于导数应用中的基本问题,证明不等式,往往通过构造函数,确定函数的最值,达到证明目的。本题利用分析法,将问题做了进一步的转化,实现了化难为易。

练习册系列答案
相关题目

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的极值.
的极值.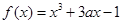 ,
, ,其中
,其中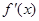 是
是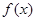 的导函数.
的导函数.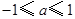 的一切
的一切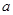 的值,都有
的值,都有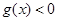 ,求实数
,求实数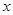 的取值范围;
的取值范围;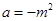 ,当实数
,当实数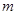 在什么范围内变化时,函数
在什么范围内变化时,函数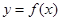 的图象与直线
的图象与直线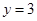 只有一个公共点.
只有一个公共点.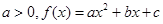 ,曲线
,曲线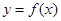 在点
在点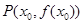 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为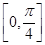 ,则点
,则点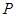 到曲线
到曲线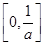
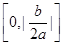
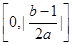
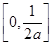
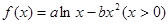
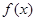 在x=1处与直线
在x=1处与直线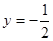 相切.
相切.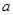 ,
,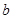 的值;②求函数
的值;②求函数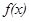 在
在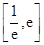 上的最大值.
上的最大值.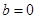 时,若不等式
时,若不等式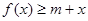 对所有的
对所有的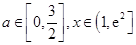 都成立,求实数
都成立,求实数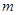 的取值范围.
的取值范围.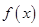 的导函数是
的导函数是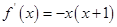 ,则函数
,则函数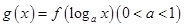 的单调递减区间是( )
的单调递减区间是( )



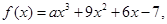 若
若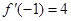 ,则a的值等于( )
,则a的值等于( )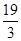
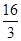
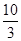
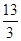

 的导函数
的导函数 .
.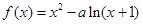 ,其中
,其中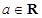 。
。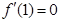 ,求a的值;
,求a的值;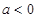 时,讨论函数
时,讨论函数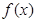 在其定义域上的单调性;
在其定义域上的单调性;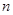 ,不等式
,不等式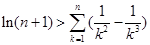 都成立。
都成立。