题目内容

（2013•东莞二模）已知数列{an}的前n项和Sn=n2-3n，若它的第k项满足2＜ak＜5，则k=（　　）
分析：先利用公式an=求出an=
S1  (n=1)
Sn-Sn-1(n≥2)
，再由第k项满足4＜ak＜7，建立不等式，求出k的值．
解答：解：已知数列{an}的前n项和Sn=n2-3n，n=1可得S1=a1=1-3=-2，
∴an=Sn-Sn-1=n2-3n-[（n-1）2-3（n-1）]=2n-4，
n=1满足an，
∴an=2n-4，
∵它的第k项满足2＜ak＜5，即2＜2k-4＜5，解得3＜k＜4.5，因为n∈N，
∴k=4，
故选C；
点评：本题考查数列的通项公式的求法，解题时要注意公式an=
S1  (n=1)
Sn-Sn-1(n≥2)
的合理运用，属于基础题．
练习册系列答案
相关题目
（2013•东莞二模）设Sn为数列{an}前n项和，对任意的n∈N*，都有Sn=2-an，数列{bn}满足bn=
bn-1
1+bn-1
，b1=2a1，
（1）求证：数列{an}是等比数列，并求{an}的通项公式；
（2）求数列{bn}的通项公式；
（3）求数列{
1
an+2bn
}的前n项和Tn．
（2013•东莞二模）命题“?x∈R，x2+1≥1”的否定是（　　）
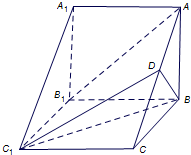（2013•东莞二模）如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．
（1）求证：AB1∥平面BC1D；
（2）若BC=3，求三棱锥D-BC1C的体积．
（2013•东莞二模）已知x＞0，y＞0，且
1
x
+
9
y
=1，则2x+3y的最小值为
29+6
6
29+6
6
．
（2013•东莞二模）已知函数f(x)=tan(
1
3
x-
π
6
)
（1）求f（x）的最小正周期；
（2）求f(
3π
2
)的值；
（3）设f(3α+
7π
2
)=-
1
2
，求
sin(π-α)+cos(α-π)
2
sin(α+
π
4
)
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网