题目内容
已知双曲线C:(1)求P的轨迹方程E;
(2)若曲线E的图象上存在点A、B,关于直线y=k(x+![]() )对称,求斜率k的取值范围.
)对称,求斜率k的取值范围.
解:(1)由已知可求得双曲线左焦点为F(-5,0)
按a平移后为P,则![]() +a
+a![]() (x,y)=(-5+λ+5,λ2)
(x,y)=(-5+λ+5,λ2)![]()
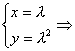 y=x2.
y=x2.
(2)设与已知直线y=k(x+![]() )垂直的直线为y=
)垂直的直线为y=![]() x+t(t为截距),
x+t(t为截距),
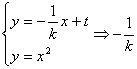 x+t=x2
x+t=x2![]() x2+
x2+![]() x-t=0,
x-t=0,
Δ=![]() +4t>0
+4t>0![]() t>
t>![]() ①
①
设点A(x1,y1),B(x2,y2).
则x1+x2=![]()
![]()
![]() ,代入直线y=
,代入直线y=![]() kx+t得
kx+t得![]() +t.
+t.
所以AB中点为(![]() +t),由对称性则将此坐标代入直线y=k(x+
+t),由对称性则将此坐标代入直线y=k(x+![]() )得
)得
![]() +t=k(
+t=k(![]() )
)![]() t=
t=![]() 2代入①得
2代入①得
![]() 3k3-2k2-1>0
3k3-2k2-1>0![]() (k-1)(3k2+k+1)>0,
(k-1)(3k2+k+1)>0,
其中方程3k2+k+1=0的Δ=1-12<0,则恒有3k2+k+1>0,
则得k>1,
所以E上存在A、B关于直线y=k(x+![]() )对称时,k的取值范围是k∈(1,+∞).
)对称时,k的取值范围是k∈(1,+∞).

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
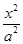 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
) -
-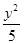 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
=1 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、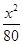 -
- =1[w~#
=1[w~#