题目内容
若P(2,-1)为曲线
(0≤θ<2π)的弦的中点,则该弦所在直线的普通方程为
|
x-y-3=0
x-y-3=0
.分析:由曲线
(0≤θ<2π),知(x-1)2+y2=25,再由P(2,-1)为曲线
(0≤θ<2π)的弦的中点,利用点差法能够求出该弦所在直线的普通方程.
|
|
解答:解:∵曲线
(0≤θ<2π),
∴(x-1)2+y2=25,
∵P(2,-1)为曲线
(0≤θ<2π)的弦的中点,
设过点P(2,-1)的弦与(x-1)2+y2=25交于A(x1,y1),B(x2,y2),
则
,
把A(x1,y1),B(x2,y2)代入(x-1)2+y2=25,
得
,
∴
,
①-②,得4(x1-x2)-2(x1-x2)-2(y1-y2)=0,
∴k=
=1,
∴该弦所在直线的普通方程为y+1=x-2,
即x-y-3=0.
故答案为:x-y-3=0.
|
∴(x-1)2+y2=25,
∵P(2,-1)为曲线
|
设过点P(2,-1)的弦与(x-1)2+y2=25交于A(x1,y1),B(x2,y2),
则
|
把A(x1,y1),B(x2,y2)代入(x-1)2+y2=25,
得
|
∴
|
①-②,得4(x1-x2)-2(x1-x2)-2(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
∴该弦所在直线的普通方程为y+1=x-2,
即x-y-3=0.
故答案为:x-y-3=0.
点评:本题考查参数方程的应用,是基础题.解题时要认真审题,注意参数方程和普通方程的相互转化和点差法的合理运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数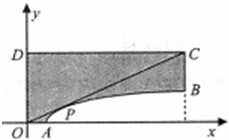 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组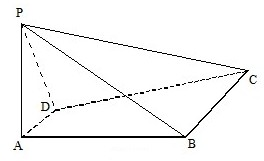 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.