题目内容
已知a>0，求证： 
－
≥a＋
－2.
－≥a＋－2.见解析
要证 －≥a＋－2，只要证 ＋2≥a＋＋.
∵a>0，故只要证
2≥
2，
即a2＋
＋4 ＋4≥a2＋2＋＋2 
＋2，
从而只要证2≥，只要证4
≥2
，
即a2＋≥2，而上述不等式显然成立，
故原不等式成立．
－≥a＋－2，只要证 ＋2≥a＋＋.∵a>0，故只要证
2≥2，即a2＋
＋4 ＋4≥a2＋2＋＋2 ＋2，从而只要证2
≥，只要证4≥2，即a2＋
≥2，而上述不等式显然成立，故原不等式成立．
练习册系列答案
相关题目
，
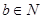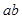能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是( )
.
，
，
。求证
中至少有一个不少于0。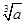
>
”假设的内容应是( )
、
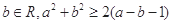”，正确的反设为
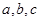满足
，则
的值