题目内容
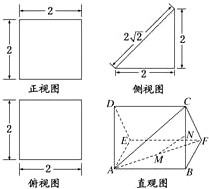
一个多面体的直观图及三视图分别如图所示(其中正视图和侧视图均为矩形,俯视图是直角三角形),M、N分别是AB1、A1C1的中点,MN AB1.
AB1.
 AB1.
AB1.
(1)求实数a的值并证明MN 平面BCC1B1;
平面BCC1B1;
(2)在上面结论下,求平面AB1C1与平面ABC所成锐二面角的余弦值
 平面BCC1B1;
平面BCC1B1;(2)在上面结论下,求平面AB1C1与平面ABC所成锐二面角的余弦值
解:(1)由图可知,ABC﹣A1B1C1为直三棱柱,侧棱CC1=a,底面为直角三角形,AC BC,AC=3,BC=4
BC,AC=3,BC=4
以C为坐标原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系,
则 ,
,
所以, ,
,
因为MN AB1,
AB1,
所以 解得:a=4
解得:a=4
此时, ,平面BCC1B1的法向量
,平面BCC1B1的法向量
∴

 与平面BCC1B1的法向量垂直,
与平面BCC1B1的法向量垂直,
且MN 平面BCC1B1
平面BCC1B1
 MN
MN 平面BCC1B1
平面BCC1B1
(2) 平面ABC的法向量 ,
,
设平面AB1C1的法向量为 ,
,
平面AB1C1与平面ABC所成锐二面角的大小等于其法向量所成锐角 的大小,
的大小,
法向量 满足:
满足:
因为A(3,0,0),C1(0,0,4),B1(0,4,4),

所以,
所以, ,
,
所以,
所以平面AB1C1与平面ABC所成锐二面角的余弦值为

 BC,AC=3,BC=4
BC,AC=3,BC=4以C为坐标原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系,
则
 ,
,所以,
 ,
,
因为MN
 AB1,
AB1,所以
 解得:a=4
解得:a=4此时,
 ,平面BCC1B1的法向量
,平面BCC1B1的法向量
∴


 与平面BCC1B1的法向量垂直,
与平面BCC1B1的法向量垂直,且MN
 平面BCC1B1
平面BCC1B1 MN
MN 平面BCC1B1
平面BCC1B1(2) 平面ABC的法向量
 ,
,设平面AB1C1的法向量为
 ,
,平面AB1C1与平面ABC所成锐二面角的大小等于其法向量所成锐角
 的大小,
的大小,法向量
 满足:
满足:
因为A(3,0,0),C1(0,0,4),B1(0,4,4),

所以,

所以,
 ,
,
所以,

所以平面AB1C1与平面ABC所成锐二面角的余弦值为



练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
 一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).

