题目内容
（本题满分10分）已知空间四边形ABCD的各边及对角线都相等，AC和平面BCD所成角的余弦值．
【解析】
试题分析：求线面角转化成线线角，即斜线与斜线在平面内的身影所成的角。然后放到三角形，解三角形。
在平面
内射影为
，所以
是
在平面上的射影，即
就是和平面所成角，在
中，求
试题解析：过点 作
垂直于平面 ，垂足为 ,
连结 ,则是在平面上的射影，
所以就是和平面所成角 2分
设空间四边形
的边长为
，连结
,
，由
, 易知
全等，
所以
,即
是
的中心 4分
在
中，可以计算出
7分
在中，
，
,即和平面所成角的余弦值为 10分
考点：线面角的求法
练习册系列答案
寒假学与练系列答案
相关题目
，
，若
，则
________.
，
，
，则：（ ）
B．
C．
D．
有两个不等实根，则实数
的取值范围是（ ）
B．
C．
D．
B．
C．
D．
在正方体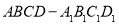
的对角线
上，过点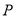
作垂直于平面
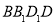的直线，与正方体表面相交于
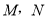．设
，
，则函数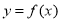
的图象大致是 （ ）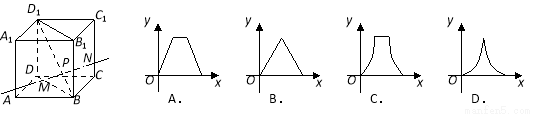
与圆
有公共点，则（ ）
B．
C．
D．
，定义了一种运算“
”，使得集合
中的元素间满足条件：如果存在元素
，使得对任意
，都有
，则称元素
是集合
，运算“
”为普通乘法；存在
，使得对任意
，都有
，所以元素
是集合
对普通乘法的单位元素．
，运算“
{
表示
阶矩阵，
}，运算“
（其中
是任意非空集合），运算“