题目内容
正四棱柱ABCD—A1B1C1D1中,底面边长为2(1)求证:平面B1EF⊥平面BDD1B1;?
(2)求点D1到平面B1EF的距离.?
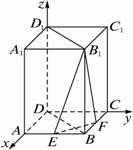
(1)证明:建立如图所示的空间直角坐标系,则D(0,0,0), B(2![]() ,2
,2![]() ,0), E(2
,0), E(2![]() ,
,![]() ,0), F(2,2
,0), F(2,2![]() ,0), D1(0,0,4), B1(2
,0), D1(0,0,4), B1(2![]() ,2
,2![]() ,4).
,4).
![]() =(-
=(-![]() ,
,![]() ,0),
,0), ![]() =(22,22,0),
=(22,22,0), ![]() =(0,0,4),
=(0,0,4),
∴![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0.
=0.
∴EF⊥DB,EF⊥DD1.
∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
(2)解析:设平面B1EF的法向量n=(x, y, z),则n⊥![]() ,n⊥
,n⊥![]() .?
.?
又![]() =(0,
=(0,![]() ,4),
,4),
∴n·![]() =-
=-![]() x+
x+![]() y=0,n·
y=0,n·![]() =
=![]() y+4z=0.
y+4z=0.
∴x=y, z=-![]() y.?
y.?
取y=1,得n=(1,1,-![]() ).
).
又D1B1=(22,22,0),∴点D1到平面B1EF的距离d=![]() =
=![]() .
.
温馨提示:利用法向量知识求点到平面的距离,必须找这个平面过这点的斜线段(如本例?D1B1).

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
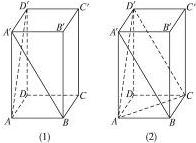 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是