题目内容
设函数f(x)=|2x+1|-|x-2|.
(1)求不等式f(x)>2的解集;
(2)若?x∈R,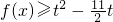 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
解:(1)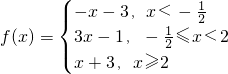
当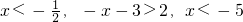 ,∴x<-5
,∴x<-5
当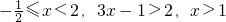 ,∴1<x<2
,∴1<x<2
当x≥2,x+3>2,x>-1,∴x≥2
综上所述 {x|x>1或x<-5}.----------------------(5分)
(2)由(1)得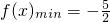 ,若?x∈R,
,若?x∈R,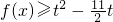 恒成立,
恒成立,
则只需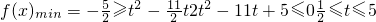 ,
,
综上所述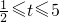 .------------------------------(10分)
.------------------------------(10分)
分析:(1)根据绝对值的代数意义,去掉函数f(x)=|2x+1|-|x-2|中的绝对值符号,求解不等式f(x)>2,
(2)由(1)得出函数f(x)的最小值,若?x∈R,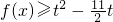 恒成立,只须
恒成立,只须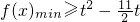 即可,求出实数t的取值范围.
即可,求出实数t的取值范围.
点评:考查了绝对值的代数意义、一元二次不等式的应用、分段函数的解析式等基本,去绝对值体现了分类讨论的数学思想,属中档题.
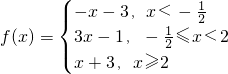
当
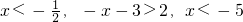 ,∴x<-5
,∴x<-5当
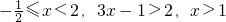 ,∴1<x<2
,∴1<x<2当x≥2,x+3>2,x>-1,∴x≥2
综上所述 {x|x>1或x<-5}.----------------------(5分)
(2)由(1)得
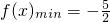 ,若?x∈R,
,若?x∈R,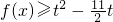 恒成立,
恒成立,则只需
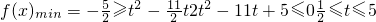 ,
,综上所述
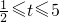 .------------------------------(10分)
.------------------------------(10分)分析:(1)根据绝对值的代数意义,去掉函数f(x)=|2x+1|-|x-2|中的绝对值符号,求解不等式f(x)>2,
(2)由(1)得出函数f(x)的最小值,若?x∈R,
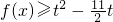 恒成立,只须
恒成立,只须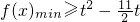 即可,求出实数t的取值范围.
即可,求出实数t的取值范围.点评:考查了绝对值的代数意义、一元二次不等式的应用、分段函数的解析式等基本,去绝对值体现了分类讨论的数学思想,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目