题目内容
 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是 ________.
正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是 ________.

分析:沿着侧棱SA把正三棱锥展开在同一个平面内,原来的点A被分到两处A、A′,则线段 AA′ 的长度即为△AMN周长的最小值.利用勾股定理求出线段 AA′ 的长度.
解答:沿着侧棱SA把正三棱锥展开在同一个平面内,原来的点A被分到两处A、A′,
则线段 AA′ 的长度即为△AMN周长的最小值.
△S AA′ 中,SA=SA′=2,∠ASA′=3×30°=90°,
∴AA′=
 =
= =2
=2 ,
,故答案为2
 .
.点评:本题考查棱锥的展开图的性质,勾股定理得应用,体现了转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正三棱锥S-ABC的三条侧棱两两互相垂直,且SA=2
,则正三棱锥S-ABC的外接球的表面积是( )
| 3 |
| A、12π | B、32π |
| C、36π | D、48π |
 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.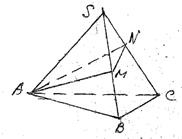 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为