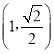题目内容
【题目】
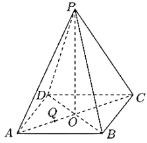
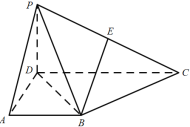
在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 中点,底面
中点,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() =90°,
=90°,![]() ,
,![]() .
.
(I)求证:![]()
![]() 平面
平面![]() ;
;
(II)求证:![]() 平面
平面![]() ;
;
(III)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 为45°.
为45°.
【答案】(I)证明见解析.
(II)证明见解析.
(III)![]()
【解析】
(I)取PD的中点F,连结EF,AF,
因为E为PC中点,所以EF//CD,且![]()
在梯形ABCD中,AB//CD,AB=1,
所以EF//AB,EF=AB,四边形ABEF为平行四边形,
所以BE//AF,
BE![]() 平面PAD,AF
平面PAD,AF![]() 平面PAD,
平面PAD,
所以BE//平面PAD.
(II)平面PCD⊥底面ABCD,PD⊥CD,所以PD⊥平面ABCD,
所以PD⊥AD.
如图,以D为原点建立空间直角坐标系D—xyz.
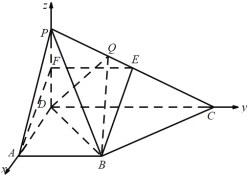
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1).
![]()
所以![]()
![]()
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.
(III)平面PBD的法向量为
![]()
![]()
所以![]() ,
,
设平面QBD的法向量为![]() =(a,b,c),
=(a,b,c),
![]() ,
,
由![]()
![]() ,
,![]()
![]() ,得
,得 ![]()
所以![]() =
=![]()
所以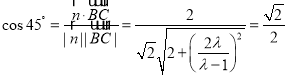
注意到![]() ,得
,得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目