题目内容
1. 为了解葫芦岛市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100),第二组[100,110),…,第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组人数为4.
为了解葫芦岛市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100),第二组[100,110),…,第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组人数为4.(1)请将频率分布直方图补充完整,并估计这组数据的平均数M;
(2)现根据初赛成绩从第四组和第六组中任意选2人,求两个人来自于同一组的概率P1;
(3)用这部分考生的成绩分布的频率估计全市考生的成绩分布,并从全市考生中随机抽取3名考生,求成绩不低于130分的人数ξ的分布列及期望.
分析 (1)令第四,第五组的频率分别为x,y,由等差中项得概念及频率和为1列关于x,y的方程组,求得x,y的值,可得频率分布直方图,进一步求得这组数据的平均数M的估计值;
(2)求出第四组和第六组人数,再由古典概型概率计算公式求得两个人来自于同一组的概率P1;
(3)求出在样本中选一人成绩不低于130分的概率为$\frac{3}{20}$,写出ξ的可能取值并求其概率,列出频率分布表,再由二项分布的期望公式求期望.
解答 解:(1)令第四,第五组的频率分别为x,y,则2y=x+0.005×10且x+y=1-(0.005+0.015+0.02+0.035)×10,
∴x=0.15,y=0.10,补充如图:
则M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5;
(2)第四组人数12,第六组人数4.
∴P1=$\frac{{C}_{12}^{2}+{C}_{4}^{2}}{{C}_{16}^{2}}$=$\frac{3}{5}$;
(3)在样本中选一人成绩不低于13(0分)的概率$\frac{3}{20}$.
ξ的可能取值0,1,2,3.
P(ξ=0)=(1-$\frac{3}{20}$)3=$\frac{4913}{8000}$,P(ξ=1)=C31(1-$\frac{3}{20}$)2$\frac{3}{20}$=$\frac{2601}{8000}$,
P(ξ=2)=C32(1-$\frac{3}{20}$)$\frac{3}{20}$2=$\frac{459}{8000}$,P(ξ=3)=$\frac{3}{20}$3=$\frac{27}{8000}$.
分布列如下:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{4913}{8000}$ | $\frac{2601}{8000}$ | $\frac{459}{8000}$ | $\frac{27}{8000}$ |
点评 本题考查频率分布直方图,考查离散型随机变量的分布列及其期望的求法,考查学生读取图表的能力,是中档题.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | ($\frac{7π}{6}$,$\frac{4π}{3}$) | B. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | C. | ($\frac{4π}{3}$,$\frac{3π}{2}$) | D. | [$\frac{4π}{3}$,$\frac{3π}{2}$] |
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
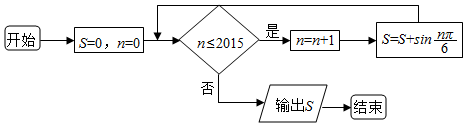
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$ |
| A. | 若α⊥β,β⊥γ,则α∥γ | B. | 若α⊥β,m∥β,则m⊥α | C. | 若m⊥α,n⊥α,则m∥n | D. | 若m∥α,n∥α,则m∥n |