题目内容
(本小题满分12分)求下列各曲线的标准方程:
(1)实轴长为12,离心率为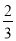 ,焦点在
,焦点在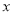 轴上的椭圆;
轴上的椭圆;
(2)抛物线的焦点是双曲线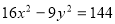 的左顶点.
的左顶点.
(1) ;(2)抛物线的标准方程为
;(2)抛物线的标准方程为 .
.
【解析】
试题分析:(1)设出椭圆的标准方程 ,根据椭圆的基本概念与条件,列出方程
,根据椭圆的基本概念与条件,列出方程 ,从中求解出
,从中求解出 即可;(2)先将双曲线的方程转化为标准方程,进而写出左顶点的坐标,结合这个点所在的坐标轴,设出抛物线的标准方程,
即可;(2)先将双曲线的方程转化为标准方程,进而写出左顶点的坐标,结合这个点所在的坐标轴,设出抛物线的标准方程, ,进而确定
,进而确定 值,即可得出抛物线的方程.
值,即可得出抛物线的方程.
试题解析:(1)设椭圆的标准方程为
由已知, ,
,

所以椭圆的标准方程为
(2)由已知,双曲线的标准方程为 ,其左顶点为
,其左顶点为
设抛物线的标准方程为 ,其焦点坐标为
,其焦点坐标为
则 即
即 ,所以抛物线的标准方程为
,所以抛物线的标准方程为 .
.
考点:1.椭圆的标准方程及其几何性质;2.抛物线的标准方程及其几何性质.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 考点3:抛物线的标准方程 考点4:抛物线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ”是“直线
”是“直线 和直线
和直线  相互平行”的( )
相互平行”的( ) ,直线
,直线 将△
将△ 分割为面积相等的两部分,则
分割为面积相等的两部分,则 ( )
( ) B.
B. C.
C. D.
D. 
 上一点
上一点 到
到 轴的距离为4,则
轴的距离为4,则 点到该抛物线焦点的距离为 .
点到该抛物线焦点的距离为 . 是减函数的区间为( )
是减函数的区间为( ) B.
B. C.
C. D.
D.
 是空间不共面的四点,且满足
是空间不共面的四点,且满足 ,则
,则 是( )
是( )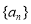 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足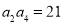 ,
,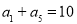 ,数列
,数列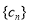 的前
的前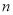 项和为
项和为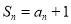
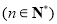 ,数列
,数列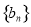 满足
满足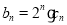 .
.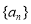 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列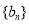 的前
的前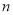 项和.
项和.