题目内容
已知四边形ABCD的顶点分别为A（1，1），B（3，-1），C（4，0），D（2，2）．
（1）试判断四边形ABCD的形状；
（2）求四边形ABCD的面积．
解：（1）∵四边形ABCD的顶点分别为A（1，1），B（3，-1），C（4，0），D（2，2），
∴
=（2，-2 ），
=（2，-2），∴=，故四边形ABCD是平行四边形，
再由
=（1，1），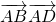
=2-2=0，可得
，故四边形ABCD是矩形．
（2）∵
=2
，
=，四边形ABCD的面积为 2×=4．
分析：（1）求出、、的坐标，可得 =，故四边形ABCD是平行四边形，再由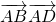=0，可得，从而得到四边形ABCD是矩形．
（2）根据=2，=，从而求得四边形ABCD的面积．
点评：本题主要考查两个向量坐标形式的运算，向量运算以及其几何意义，两个向量垂直的性质，属于基础题．
∴
=（2，-2 ），=（2，-2），∴=，故四边形ABCD是平行四边形，再由
=（1，1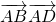），=2-2=0，可得，故四边形ABCD是矩形．（2）∵
=2，=，四边形ABCD的面积为 2×=4．分析：（1）求出
、、的坐标，可得 =，故四边形ABCD是平行四边形，再由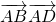=0，可得，从而得到四边形ABCD是矩形．（2）根据
=2，=，从而求得四边形ABCD的面积．点评：本题主要考查两个向量坐标形式的运算，向量运算以及其几何意义，两个向量垂直的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知四边形ABCD的三个顶点A（0，2），B（-1，-2），C（3，1），且
=2
，则顶点D的坐标为（ ）
| BC |
| AD |
A、(2，
| ||
B、(2，-
| ||
| C、（3，2） | ||
| D、（1，3） |
（1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．