题目内容
已知0＜α＜π，且sinα+cosα=
，求值：
（1）sinαcosα；
（2）
．
| 7 |
| 13 |
（1）sinαcosα；
（2）
| 2sin2α+3cos2α |
| sin2α+sinαcosα |
分析：（1）利用原式的配方并化简可算出结果．
（2）构造一元二次方程，得到2解，带入化简即可．
（2）构造一元二次方程，得到2解，带入化简即可．
解答：（1）∵（sinα+cosα）2=(
)2
∴sinαcosα=-
（2）∵0＜α＜π 且sinαcosα的值为负数
∴α为第二象限角
即sinα为正数，cosα为负数
又∵sinα+cosα=
，sinαcosα=-
构造一个二次函数，sinα，cosα分别是函数的两个解
即x2-
x-
=0
解得：sinα=
，cosα=-
带入原式化简得：
=
| 7 |
| 13 |
∴sinαcosα=-
| 60 |
| 169 |
（2）∵0＜α＜π 且sinαcosα的值为负数
∴α为第二象限角
即sinα为正数，cosα为负数
又∵sinα+cosα=
| 7 |
| 13 |
| 60 |
| 169 |
构造一个二次函数，sinα，cosα分别是函数的两个解
即x2-
| 7 |
| 13 |
| 60 |
| 169 |
解得：sinα=
| 12 |
| 13 |
| 5 |
| 13 |
带入原式化简得：
| 2sin2α+3cos2α |
| sin2α+sinαcosα |
| 263 |
| 84 |
点评：此题考查了三角函数与一元二次方程之间转换，属于中档题..
练习册系列答案
津桥教育计算小状元系列答案
相关题目
的周期为
，且当
时，函数
的最小值为0．
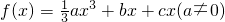，已知a＜b＜c，且
，曲线y=f（x）在x=1处取极值．