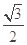题目内容
已知函数f(x)=sin(2x+
)+sin(2x-
)+2cos2x.
(Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)求使f(x)≥2的x的取值范围.
| π |
| 6 |
| π |
| 6 |
(Ⅰ)求f(x)的最小正周期和单调递增区间;
(Ⅱ)求使f(x)≥2的x的取值范围.
(Ⅰ)∵sin(2x+
)=sin2xcos
+cos2xsin
,
sin(2x-
)=sin2xcos
-cos2xsin
,cos2x=
(cos2x+1)
∴f(x)=sin(2x+
)+sin(2x-
)+2cos2x
=sin2xcos
+cos2xsin
+sin2xcos
-cos2xsin
+cos2x+1
=
sin2x+cos2x+1=2sin(2x+
)+1
可得f(x)的最小正周期T=
=
=π.
令-
+2kπ≤2x+
≤
+2kπ(k∈Z),解之得-
+kπ≤x≤
+kπ(k∈Z),
∴函数f(x)的递增区间是[-
+kπ,
+kπ],k∈Z.
(Ⅱ)由f(x)≥2,得2sin(2x+
)+1≥2(k∈Z),即sin(2x+
)≥
,
根据正弦函数的图象,可得
+2kπ≤2x+
≤
+2kπ(k∈Z),
解之得kπ≤x≤kπ+
(k∈Z),
∴使不等式f(x)≥2成立的x取值范围是{x|kπ≤x≤kπ+
,k∈Z}.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
sin(2x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴f(x)=sin(2x+
| π |
| 6 |
| π |
| 6 |
=sin2xcos
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| 3 |
| π |
| 6 |
可得f(x)的最小正周期T=
| 2π |
| |ω| |
| 2π |
| 2 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数f(x)的递增区间是[-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)由f(x)≥2,得2sin(2x+
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
根据正弦函数的图象,可得
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解之得kπ≤x≤kπ+
| π |
| 3 |
∴使不等式f(x)≥2成立的x取值范围是{x|kπ≤x≤kπ+
| π |
| 3 |

练习册系列答案
相关题目
 ,
,  ,则
,则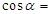 。
。 是
是 边
边 延长线上一点,记
延长线上一点,记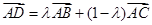 . 若关于
. 若关于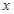 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数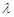 的取值范围是( )
的取值范围是( )
 或
或
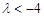 或
或 的值为( )
的值为( )