题目内容
已知 是定义在
是定义在 上的增函数,
上的增函数, ,
, .
.
(1)求证: ;
;
(2)求 的值;
的值;
(3)若 ,求
,求 的取值范围.
的取值范围.
(1)详见试题分析;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)(赋值法)令 即可得证;(2)(赋值法)令
即可得证;(2)(赋值法)令 即得;(3)通过赋值得
即得;(3)通过赋值得 ,再利用已知条件、函数单调性,去掉函数符号得到不等式,其中注意各个函数都要有意义,都在定义域范围内.
,再利用已知条件、函数单调性,去掉函数符号得到不等式,其中注意各个函数都要有意义,都在定义域范围内.
试题解析:(1)令 ,带入
,带入 中,得
中,得 ;
;
(2)令 ,得
,得 ;
;
(3)令 ,得
,得 ,则
,则 ,
,
所以 ,解得
,解得 .
.
考点:(1)、(2)抽象函数证明、计算中的赋值法; (3)抽象函数不等式解法.

练习册系列答案
相关题目
 ,则
,则
 B.
B.
 D.
D.
 中,
中, ,则
,则 .
. 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,则该双曲线的焦点到其渐近线的距离为 .
的焦点重合,则该双曲线的焦点到其渐近线的距离为 . ,且
,且 ,则
,则 .
. 的定义域为
的定义域为 ,则函数
,则函数 的定义域是 .
的定义域是 . 的结果等于( )
的结果等于( ) B.
B. C.
C. D.
D.
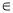 [-1,1],函数
[-1,1],函数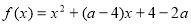 的值恒大于零,则x的取值范围是( )
的值恒大于零,则x的取值范围是( )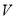 ,那么其表面积最小时,底面边长为( )
,那么其表面积最小时,底面边长为( )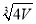 B.
B.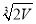 C.
C.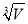 D.
D.