题目内容
如图：平行四边形
的周长为8，点
的坐标分别为
．
（Ⅰ）求点
所在的曲线方程；
（Ⅱ）过点
的直线
与(Ⅰ)中曲线交于点
，与y轴交于点
，
且//
，求证：
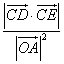为定值．
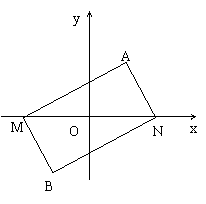
解：（Ⅰ）因为四边形是平行四边形,周长为8
所以两点到的距离之和均为4,可知所求曲线为椭圆 …………1分
由椭圆定义可知，
，
所求曲线方程为
…………………4分
（Ⅱ）由已知可知直线的斜率存在，又直线过点
设直线的方程为：
…………………5分
代入曲线方程
，并整理得
点在曲线上,所以(
,
) …………………8分
,
,
…………………9分
因为//,
所以设的方程为
…………………10分
代入曲线方程，并整理得
所以
…………………11分
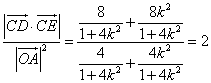
所以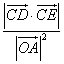： 为定值 …………………13分
练习册系列答案
阅读快车系列答案
相关题目
的两条对角线相交于点
，点
是
中点，若
，
,且
，则
的值为
B．
C．
D．
的两条对角线相交于点
，点
是
的中点. 若
， 
，且
，则
. 
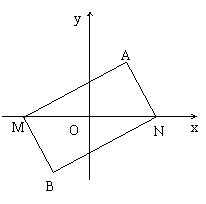如图：平行四边形
的周长为8，点
的坐标分别为
．
所在的曲线方程；
的直线
与(Ⅰ)中曲线交于点
，与Y 轴交于点
，且
，求证：
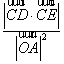为定值．
如图：平行四边形
的周长为8，点
的坐标分别为
．
所在的曲线方程；
的直线
与(Ⅰ)中曲线交于点
，与Y 轴交于点
，且
，求证：
为定值．