题目内容
若tanθ=2,则
=
| cosθ-sinθ |
| sinθ+cosθ |
-
| 1 |
| 3 |
-
.| 1 |
| 3 |
分析:根据tanθ=
,得出sinθ=2cosθ,代入所求式子即可即可得出答案.
| sinθ |
| cosθ |
解答:解:∵tanθ=2
∴tanθ=
=2,即sinθ=2cosθ,
∴
=
=-
故答案为:-
∴tanθ=
| sinθ |
| cosθ |
∴
| cosθ-sinθ |
| sinθ+cosθ |
| cosθ-2cosθ |
| 2cosθ+cosθ |
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:此题考查了同角三角函数的基本关系,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目




 的值为( )
的值为( )

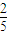
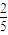
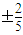
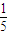
 的值为( )
的值为( )
