题目内容
已知向量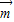 =(
=(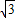 sinx,cosx),
sinx,cosx),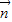 =(cosx,cosx),
=(cosx,cosx),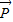 =(2
=(2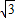 ,1).
,1).(1)若
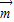
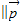 ,求
,求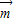 •
•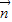 的值;
的值;(2)若f(x)=
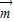 •
•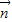 ,求f(x)最小正周期及f(x)在(0,
,求f(x)最小正周期及f(x)在(0,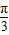 ]的值域.
]的值域.
【答案】分析:(1)根据向量共线的坐标关系建立等式,可求出tanx的值,然后根据数量积公式表示出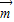 •
•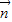 ,最后转化成tanx的表达式,从而可求出所求;
,最后转化成tanx的表达式,从而可求出所求;
(2)利用二倍角公式和辅助角公式将函数化成Asin(ωx+φ)+B的形式,利用正弦函数的性质可求出函数的周期和值域.
解答:解;(1)若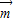 ∥
∥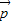 ,∴
,∴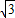 sinx-2
sinx-2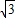 cosx=0
cosx=0
∴tanx=2 …(3分)
∴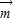 •
•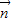 =
=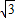 sinxcosx+cosxcosx
sinxcosx+cosxcosx
=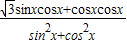
=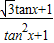
=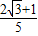 …(6分)
…(6分)
(2)f(x)=sin(2x+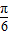 )+
)+ ,∴T=π …(9分)
,∴T=π …(9分)
∵x∈(0,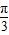 ]
]
∴2x+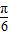 ∈(
∈(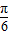 ,
,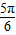 ]则sin(2x+
]则sin(2x+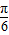 )∈[
)∈[ ,1]
,1]
∴f(x)∈[1, ],即函数f(x)=
],即函数f(x)=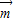 •
•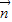 的值域为[1,
的值域为[1, ]…(12分)
]…(12分)
点评:本题主要考查了向量的数量积,以及二倍角公式和辅助角公式,同时考查了转化的思想和运算求解的能力,属于中档题.
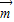 •
•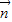 ,最后转化成tanx的表达式,从而可求出所求;
,最后转化成tanx的表达式,从而可求出所求;(2)利用二倍角公式和辅助角公式将函数化成Asin(ωx+φ)+B的形式,利用正弦函数的性质可求出函数的周期和值域.
解答:解;(1)若
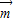 ∥
∥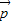 ,∴
,∴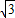 sinx-2
sinx-2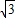 cosx=0
cosx=0∴tanx=2 …(3分)
∴
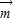 •
•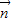 =
=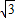 sinxcosx+cosxcosx
sinxcosx+cosxcosx=
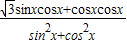
=
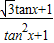
=
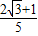 …(6分)
…(6分)(2)f(x)=sin(2x+
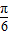 )+
)+ ,∴T=π …(9分)
,∴T=π …(9分)∵x∈(0,
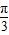 ]
]∴2x+
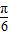 ∈(
∈(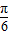 ,
,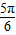 ]则sin(2x+
]则sin(2x+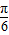 )∈[
)∈[ ,1]
,1]∴f(x)∈[1,
 ],即函数f(x)=
],即函数f(x)=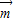 •
•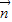 的值域为[1,
的值域为[1, ]…(12分)
]…(12分)点评:本题主要考查了向量的数量积,以及二倍角公式和辅助角公式,同时考查了转化的思想和运算求解的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(sinx,cosx),向量
=(1,
),则|
+
|的最大值为( )
| a |
| b |
| 3 |
| a |
| b |
| A、3 | ||
B、
| ||
| C、1 | ||
| D、9 |