题目内容
设椭圆M: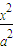 +
+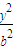 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为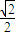 ,点A(a,0),B(0,-b),原点O到直线AB的距离为
,点A(a,0),B(0,-b),原点O到直线AB的距离为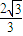 .
.(Ⅰ)求椭圆M的方程;
(Ⅱ)设直线l:y=2x+m与椭圆M相交于C、D不同两点,经过线段CD上点E的直线与y轴相交于点P,且有
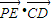 =0,|
=0,|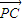 |=|
|=|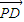 |,试求△PCD面积S的最大值.
|,试求△PCD面积S的最大值.
【答案】分析:(Ⅰ)由 得a=
得a=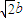 .可得直线AB的方程为
.可得直线AB的方程为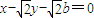 ,于是
,于是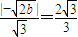 ,由此能够求出椭圆M的方程.
,由此能够求出椭圆M的方程.
(Ⅱ)设C(x1,y1),D(x2,y2),由方程组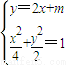 ,得9x2+8mx+2m2-4=0,所以有
,得9x2+8mx+2m2-4=0,所以有 ,
,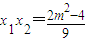 ,且△≥0,即m2≤18.
,且△≥0,即m2≤18.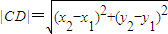 =
=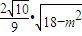 .由
.由 ,E是线段CD的中点,由此能求出S的最大值.
,E是线段CD的中点,由此能求出S的最大值.
解答:解:(Ⅰ)由 得a=
得a= (2分)
(2分)
可得直线AB的方程为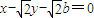 ,于是
,于是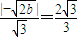 ,
,
得b=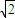 ,b2=2,a2=4,所以椭圆M的方程为
,b2=2,a2=4,所以椭圆M的方程为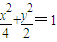 (2分)
(2分)
(Ⅱ)设C(x1,y1),D(x2,y2),由方程组 ,
,
得9x2+8mx+2m2-4=0,
所以有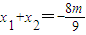 ,
,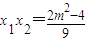 ,且△≥0,即m2≤18.(2分)
,且△≥0,即m2≤18.(2分)
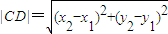
=
=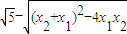
=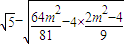
= .(2分)
.(2分)
因为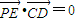 ,
,
所以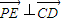 ,
,
又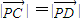 ,
,
所以E是线段CD的中点,
点E的坐标为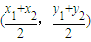 ,即E的坐标是
,即E的坐标是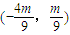 ,
,
因此直线PE的方程为y=-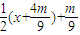 ,得点P的坐标为(0,-
,得点P的坐标为(0,-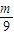 ),
),
所以|PE|=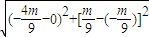
=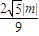 .(2分)
.(2分)
因此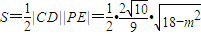
=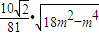 .
.
所以当m2=9,即m=±3时,S取得最大值,最大值为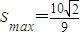 .
.
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.
 得a=
得a=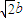 .可得直线AB的方程为
.可得直线AB的方程为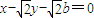 ,于是
,于是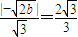 ,由此能够求出椭圆M的方程.
,由此能够求出椭圆M的方程.(Ⅱ)设C(x1,y1),D(x2,y2),由方程组
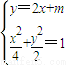 ,得9x2+8mx+2m2-4=0,所以有
,得9x2+8mx+2m2-4=0,所以有 ,
,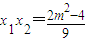 ,且△≥0,即m2≤18.
,且△≥0,即m2≤18.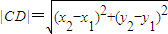 =
=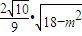 .由
.由 ,E是线段CD的中点,由此能求出S的最大值.
,E是线段CD的中点,由此能求出S的最大值.解答:解:(Ⅰ)由
 得a=
得a= (2分)
(2分)可得直线AB的方程为
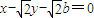 ,于是
,于是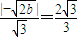 ,
,得b=
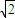 ,b2=2,a2=4,所以椭圆M的方程为
,b2=2,a2=4,所以椭圆M的方程为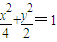 (2分)
(2分)(Ⅱ)设C(x1,y1),D(x2,y2),由方程组
 ,
,得9x2+8mx+2m2-4=0,
所以有
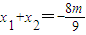 ,
,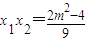 ,且△≥0,即m2≤18.(2分)
,且△≥0,即m2≤18.(2分)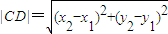
=

=
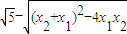
=
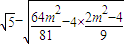
=
 .(2分)
.(2分)因为
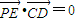 ,
,所以
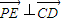 ,
,又
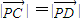 ,
,所以E是线段CD的中点,
点E的坐标为
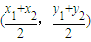 ,即E的坐标是
,即E的坐标是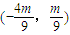 ,
,因此直线PE的方程为y=-
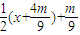 ,得点P的坐标为(0,-
,得点P的坐标为(0,-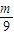 ),
),所以|PE|=
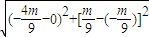
=
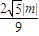 .(2分)
.(2分)因此
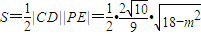
=
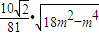 .
.所以当m2=9,即m=±3时,S取得最大值,最大值为
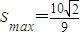 .
.点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
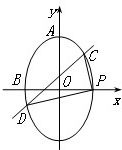 设椭圆M:
设椭圆M: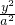 +
+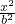 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,点A(0,a),B(-b,0),原点O到直线AB的距离为
,点A(0,a),B(-b,0),原点O到直线AB的距离为 ,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且
,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且 ⊥
⊥ .
. +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,点A(0,a),B(-b,0),原点O到直线AB的距离为
,点A(0,a),B(-b,0),原点O到直线AB的距离为 ,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且
,P是椭圆的右顶点,直线l:x=my-n与椭圆M相交于C,D两点,且 ⊥
⊥ .
.