题目内容
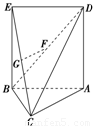
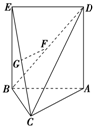
如图△ABC中,AC=BC=![]() AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.
AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.
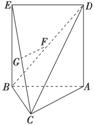
(1)求证:GF∥平面ABC;
(2)求证:平面EBC⊥平面ACD;
(3)求几何体ADEBC的体积V.
解:
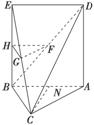
(1)证明:如图,取BE的中点H,连接HF,GH.
∵G,F分别是EC和BD的中点,
∴HG∥BC,HF∥DE.
又∵四边形ADEB为正方形,
∴DE∥AB,从而HF∥AB.
∴HF∥平面ABC,HG∥平面ABC.
∴平面HGF∥平面ABC.
∴GF∥平面ABC.
(2)证明:∵ADEB为正方形,∴EB⊥AB.
又∵平面ABED⊥平面ABC,
∴BE⊥平面ABC.
∴BE⊥AC.
又∵CA2+CB2=AB2,∴AC⊥BC.
∴AC⊥平面BCE.
从而平面EBC⊥平面ACD.
(3)取AB的中点N,连接CN,∵AC=BC,
∴CN⊥AB,且CN=![]() AB=
AB=![]() a.
a.
又平面ABED⊥平面ABC,
∴CN⊥平面ABED.
∵C-ABED是四棱锥,
∴VC-ABED=![]() SABED·CN=
SABED·CN=![]() a2·
a2·![]() a=
a=![]() a3.
a3.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图△ABC中,AC=BC=
如图△ABC中,AC=BC=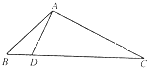 如图△ABC中,已知点D在BC边上,满足
如图△ABC中,已知点D在BC边上,满足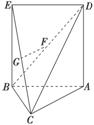
 AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.
AB,四边形ABED是边长为a的正方形,平面ABED⊥平面ABC,若G、F分别是EC、BD的中点.