题目内容
设函数
(1)当
时,求不等式
的解集;
(2)若对
恒成立,求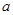
的取值范围.
(1)当
时,求不等式的解集; (2)若
对恒成立,求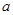的取值范围.（1）
（2）
（2）试题分析：(1) 当
时, 
，分段讨论可得不等式
的解集为 (2) 根据绝对值的几何意义可知，
，由题意得
, 解得点评：解决含绝对值的不等式问题，最主要的是分类讨论去掉绝对值号，讨论时要做到不重不漏；而绝对值的几何意义也是经常考查的内容，要灵活应用.
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
，
，
．求证：
．
满足不等式
则实数
的取值范围是__________.
的解集。
的最小值为
；
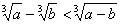成立，则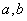
应满足的条件是
且
且