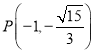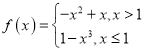题目内容
【题目】已知函数
(1)求
的最小正周期；
(2)设
为锐角三角形,角A的对边长
角B的对边长
若
求的面积.
【答案】（1）π（2）
【解析】
（1）利用三角恒等变换化简函数的解析式，再根据正弦函数的周期性，得出结论．
（2）根据f（A）＝0，求得A的值，再利用正弦定理求得B，可得C的值，利用△ABC的面积为 
absinC，计算求得结果．
解：（1）函数f（x）＝sinxcosx﹣sin2x＝sin2x﹣
＝
sin（2x+
）﹣，
故它的最小正周期为
＝π．
（2）∵△ABC为锐角三角形，角A的对边长
，角B的对边长
，
若f（A）＝sin（2A+）﹣＝0，
∴sin（2A+）＝，∴2A+＝
，∴A＝．
再由正弦定理可得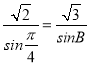
，∴sinB＝
，
∴B＝
，∴C＝π﹣A﹣B＝
，
∴sinC＝sin（
+）＝sincos+cossin＝
＝
，
故△ABC的面积为 absinC＝＝．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
【题目】通过随机询问100名性别不同的大学生是否爱好某项运动，得到如下
列联表：
（1）能否有
的把握认为是否爱好该项运动与性别有关？请说明理由．
（2）利用分层抽样的方法从以上爱好该项运动的大学生中抽取6人组建“运动达人社”，现从“运动达人社”中选派2人参加某项校际挑战赛，求选出的2人中恰有1名女大学生的概率．
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 15 | 25 | 40 |
总计 | 55 | 45 | 100 |
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
，其中
