Question

(本题满分16分)

       设函数f(x)=ax³-(a+b)x²+bx+c，其中a＞0，b，c∈R．

       (1)若=0，求函数f(x)的单调增区间；

(2)求证：当0≤x≤1时，||≤．(注：max{a，b}表示a，b中的最大值)

Answer 1

解：(1)由=0，得a=b． …………………………………………………………1分

故f(x)= ax³－2ax²+ax+c．

由=a(3x²－4x+1)=0，得x₁=，x₂=1．…………………………………………2分

列表：

x	(-∞，)		(，1)	1	(1，+∞)
	+	0	-	0	+
f(x)	增	极大值	减	极小值	增

由表可得，函数f(x)的单调增区间是(-∞，)及(1，+∞) ．…………………………4分

(2)=3ax²-2(a+b)x+b=3．

①当时，则在上是单调函数，

所以≤≤，或≤≤，且+=a>0．

所以||≤．………………………………………………………8分

②当，即-a＜b＜2a，则≤≤．

(i) 当-a＜b≤时，则0＜a+b≤．

所以  ＝＝≥＞0．

所以 ||≤． ……………………………………………………12分

(ii) 当＜b＜2a时，则＜0，即a²+b²－＜0．

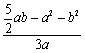所以=＞＞0，即＞．

所以  ||≤．

综上所述：当0≤x≤1时，||≤．……………………………16分