题目内容
设a、b、c均为实数，求证：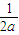
+
+
≥
+
+
．
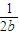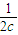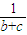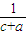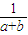【答案】分析：对左边变形
（
+
）+
（
+
）+
（
+
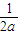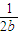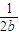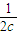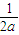）后两项两项地应用基本不等式，得到三个不等式后相加即得．
解答：证明：∵a、b、c均为实数，
∴
（
+
）≥
≥
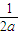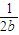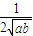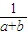，当a=b时等号成立；
（
+
）≥
≥
，
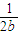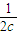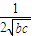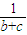当b=c时等号成立；
（
+
）≥
≥
．
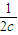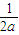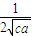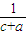三个不等式相加即得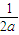
+
+
≥
+
+
，
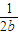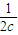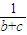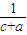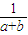当且仅当a=b=c时等号成立．
点评：从已知条件出发，利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式，这个证明方法叫综合法．
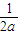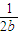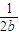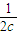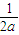（+）+（+）+（+）后两项两项地应用基本不等式，得到三个不等式后相加即得．解答：证明：∵a、b、c均为实数，
∴
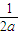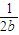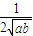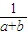（+）≥≥，当a=b时等号成立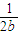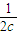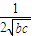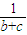；（+）≥≥，当b=c时等号成立；
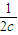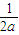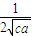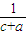（+）≥≥．三个不等式相加即得
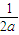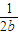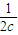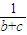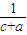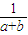++≥++，当且仅当a=b=c时等号成立．
点评：从已知条件出发，利用定义、公理、定理、某些已经证明过的不等式及不等式的性质经过一系列的推理、论证等而推导出所要证明的不等式，这个证明方法叫综合法．
练习册系列答案
一本好题口算题卡系列答案
相关题目
+
+
≥
+
+
．
+
+
≥
+
+
．
+
+
≥
+
+
．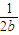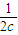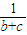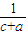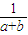