题目内容
已知函数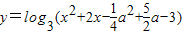
的定义域为R（1）求a的取值范围；
（2）若函数g（a）=2+log2a+log2a×|log2a-3|，求g（a）的值域．
【答案】分析：（1）由题意可得二次函数t=x2+2x-
a2+
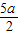-3 的判别式 
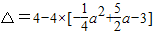=a2-10a+16＜0，解此一元二次不等式求得a的取值范围．
（2）令t=log2a，则t∈（1，3），故 g（a）=h（t）=2+t+t|t-3|=-（t-2）2+6，利用二次函数的性质求得g（a）的值域．
解答：解：（1）由于函数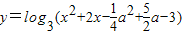
的定义域为R，故对于二次函数t=x2+2x-
a2+
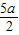-3，
依题意可得它的判别式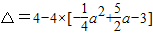
=a2-10a+16＜0，解得2＜a＜8，故a的取值范围为（2，8）．
（2）令t=log2a，则t∈（1，3），故 g（a）=h（t）=2+t+t|t-3|=-t2+4t+2=-（t-2）2+6，
当t∈（1，3）时，由二次函数的性质可得h（t）∈（5，6]，
所以g（a）的值域为（5，6]．
点评：本题主要考查指数型复合函数的性质，求二次函数在闭区间上的最值，属于中档题．
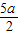a2+-3 的判别式 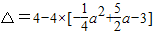=a2-10a+16＜0，解此一元二次不等式求得a的取值范围．（2）令t=log2a，则t∈（1，3），故 g（a）=h（t）=2+t+t|t-3|=-（t-2）2+6，利用二次函数的性质求得g（a）的值域．
解答：解：（1）由于函数
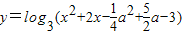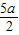的定义域为R，故对于二次函数t=x2+2x-a2+-3，依题意可得它的判别式
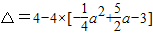=a2-10a+16＜0，解得2＜a＜8，故a的取值范围为（2，8）．（2）令t=log2a，则t∈（1，3），故 g（a）=h（t）=2+t+t|t-3|=-t2+4t+2=-（t-2）2+6，
当t∈（1，3）时，由二次函数的性质可得h（t）∈（5，6]，
所以g（a）的值域为（5，6]．
点评：本题主要考查指数型复合函数的性质，求二次函数在闭区间上的最值，属于中档题．
练习册系列答案
相关题目
的定义域为R，且当
时，
恒成立，
对称；
图象的一个对称点。
的定义域为R，当
时，
，且对任意的实数
R，等式
成立．若数列
满足
，且
N*)，则
的值为（ ）
的定义域为R，它的反函数为
，如果
与
互为反函数，且
，则
的值为（
）
B、0
C、
D、
的定义域为R,当
时,
,且对任意的实数
R,等式
成立.若数列
满足
,且
(
N*),则
的值为（ ）