题目内容
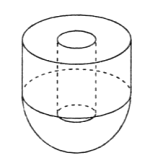
【题目】如图所示，某几何体由底面半径和高均为5的圆柱与半径为5的半球面对接而成，该封闭几何体内部放入一个小圆柱体，且圆柱体的上下底面均与外层圆柱的底面平行，则小圆柱体积的最大值为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
小圆柱的底面半径为r (0
r5)，小圆柱的高分为2部分，上半部分在大圆柱内为5，下半部分深入半球内为h (0h5)，由于下半部分截面
和球的半径构成直角三角形，即
+
，从而可以找出体积表达式进而利用函数知识求出最值。
小圆柱的高分为上下两部分，上部分同大圆柱一样为5，下部分深入底部半球内设为h (0h5)，小圆柱的底面半径设为r (0r5)，由于和球的半径构成直角三角形，即+，所以小圆柱体积
，(0h5)，求导
，当0h
时，体积
单调递增，当
h5时，体积单调减。所以当h=
时，小圆柱体积取得最大值，
，故选B.
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
【题目】2019年某地遭遇严重干旱，某乡计划向上级申请支援，为上报需水量，乡长事先抽样调查100户村民的月均用水量，得到这100户村民月均用水量（单位：t）的频率分布表如下：
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
（1）请完成该频率分布表，并画出相对应的频率分布直方图.
（2）样本的中位数是多少？
（3）已知上级将按每户月均用水量向该乡调水，若该乡共有1200户，请估计上级支援该乡的月调水量是多少吨.
