题目内容
知x、y、z均为实数，
（1）若x+y+z=1,求证：
+
+
≤3
；
（2）若x+2y+3z=6，求x2+y2+z2的最小值.
（1）证明略（2）x2+y2+z2的最小值为
解析:
（1）证明 因为（
+
+
）2
≤(12+12+12)(3x+1+3y+2+3z+3)=27.
所以++≤3
. 7分
(2)解 因为(12+22+32)(x2+y2+z2)
≥(x+2y+3z)2=36,
即14(x2+y2+z2)≥36,
所以x2+y2+z2的最小值为
. 14分
练习册系列答案
相关题目
-
＜
；
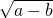，b=y2-2z+
，c=z2-2x+
求证：a，b，c中至少有一个大于0．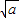
-
＜
；
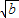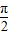，b=y2-2z+
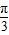，c=z2-2x+
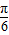求证：a，b，c中至少有一个大于0．
-
＜
；
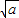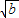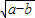，b=y2-2z+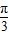
，c=z2-2x+
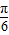求证：a，b，c中至少有一个大于0．