题目内容
7.在△ABC中,a,b,c分别为角A、B、C所对的边,且满足3=b2-c2,又sinBcosC=2cosBsinC,则边长a的值为3.分析 利用正弦定理,余弦定理化简已知等式可得3b2=a2+3c2,联立3=b2-c2,即可解得a的值.
解答 解:∵sinBcosC=2cosBsinC,
∴由正弦定理可得:bcosC=2ccosB,
结合余弦定理可得:b•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=2c•$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
∴整理可得:3b2=a2+3c2,
又∵3=b2-c2,
∴联立解得:a2=9,即a=3.
故答案为:3.
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
12.对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用的流量统计到各组的频率视为概率,并假设每天手机的日流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.
 .
. ,求函数
,求函数 在
在 处切线方程;
处切线方程; ,
, ,则
,则 等于( )
等于( ) B.
B.
 D.
D.

 为正相关,
为正相关, 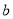 为负相关,
为负相关, 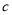 为不相关
为不相关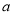 为负相关,
为负相关,  为不相关,
为不相关, 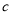 为正相关
为正相关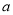 为负相关,
为负相关,  为正相关,
为正相关,  为不相关
为不相关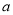 为正相关,
为正相关,  为不相关,
为不相关,  为负相关
为负相关