题目内容
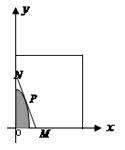 某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线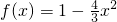 的一部分,栏栅与矩形区域的边界交于点M,N,交曲线于点P,则△OMN(O为坐标原点)的面积的最小值为________.
的一部分,栏栅与矩形区域的边界交于点M,N,交曲线于点P,则△OMN(O为坐标原点)的面积的最小值为________.

分析:求导函数,设出P的坐标,确定过点P的切线方程,进而可得M,N的坐标,表示出三角形的面积,利用导数法,即可确定△OMN(O为坐标原点)的面积的最小值.
解答:求导函数,可得

设P(m,
 )(m>0),则过点P的切线方程为y-(
)(m>0),则过点P的切线方程为y-( )=
)= ×(x-m)
×(x-m)令y=0,则x=
 ,令x=0,则y=1+
,令x=0,则y=1+
∴△OMN(O为坐标原点)的面积为S=
 =
=
求导函数可得S′=

令S′=0,可得16m4+8m2-3=0
∴m=

∴m>
 时,函数单调增,0<m<
时,函数单调增,0<m< 时,函数单调减
时,函数单调减∴m=
 时,函数取得极小值且为最小值,最小值为
时,函数取得极小值且为最小值,最小值为
故答案为:
 .
.点评:本题考查导数知识的运用,解题的关键是确定切线方程,求出三角形的面积,利用导数法求最值,属于中档题.

练习册系列答案
相关题目
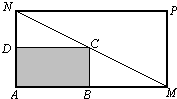 (2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
(2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
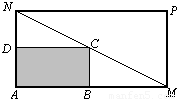 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.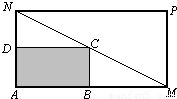 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米. 某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.