题目内容
已知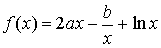 在x=-1,x=
在x=-1,x=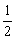 处取得极值.(1)求a、b的值;
处取得极值.(1)求a、b的值;
(2)若对x∈[ ,4]时,
,4]时, >c恒成立,求c的取值范围.
>c恒成立,求c的取值范围.
解:(1)∵f(x)=2ax- +lnx, ∴f′(x)=2a+
+lnx, ∴f′(x)=2a+ +
+ .
.
∵f(x)在x=-1与x=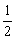 处取得极值,∴f′(-1)=0,f′(
处取得极值,∴f′(-1)=0,f′(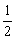 )=0,
)=0,
即 解得
解得 ∴所求a、b的值分别为1、-1.
∴所求a、b的值分别为1、-1.
(2)由(1)得f′(x)=2- +
+ =
= (2x2+x-1)=
(2x2+x-1)= (2x-1)(x+1).
(2x-1)(x+1).
∴当x∈[ ,
,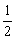 ]时,f′(x)<0;当x∈[
]时,f′(x)<0;当x∈[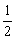 ,4]时,f′(x)>0.∴f(
,4]时,f′(x)>0.∴f(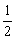 )是f(x)在[
)是f(x)在[ ,4]上的极小值.又∵只有一个极小值,
,4]上的极小值.又∵只有一个极小值,
∴f(x)min=f(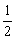 )=3-ln2.
)=3-ln2.
∵f(x)>c恒成立,∴c<f(x)min=3-ln2.
∴c的取值范围为c<3-ln2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的零点的个数是 个.
的零点的个数是 个. 则
则 且
且 ”的逆命题、否命题及逆否命题,并判断它们的真假.
”的逆命题、否命题及逆否命题,并判断它们的真假.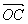 =α
=α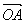 +β
+β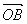 ,其中α,β
,其中α,β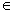 R,α+β=1,则点C的轨迹为( )
R,α+β=1,则点C的轨迹为( )  为中点的抛物线
为中点的抛物线 的弦所在直线方程为: .
的弦所在直线方程为: . 
 B.
B.
 D.
D.
 -m,若对∀x1∈[-1,3],∃x2∈[0,2], f(x1)≥g(x2),则实数m的取值范围是________.
-m,若对∀x1∈[-1,3],∃x2∈[0,2], f(x1)≥g(x2),则实数m的取值范围是________.