题目内容
(10分)对于函数![]() ,若存在实数
,若存在实数![]() 使
使![]() 成立,则称点
成立,则称点![]() 为函数的一个不动点.
为函数的一个不动点.
(1)若![]() ,求函数f(x)的不动点;
,求函数f(x)的不动点;
(2)若对于任意实数b,函数![]() 总有两个相异的不动点,求实数a的取值范围;
总有两个相异的不动点,求实数a的取值范围;
(3)若定义在实数集R上的函数![]() 恒满足
恒满足![]() ,且存在n
,且存在n![]() 个不动点,设
个不动点,设![]() ,求函数
,求函数![]() 的最小值.
的最小值.
答案:
解析:
解析:
解:(1)由x2-x=x得x=0或x=2 \f(x)的不动点为(0,0)和(2,2)………2分 (2)由题意可知 ax2+bx-1=x有两个相异实根 ax2+(b-1)x-1=0有两个相异实根 显然a¹0 \D=(b-1)2+4a>0对bÎR恒成立 ……………4分 即 又 \a>0 即a的取值范围为(0,+∞) …………………6分 (3)∵f(x)为R上的奇函数 \ f(0)=0 即(0,0)为f(x)的一个不动点 又设x0(x0¹0)满足f(x) = x 即f(x0) = x0 \ f(-x0) =- f(-x0) =- x0 即若点(x0,y0)为f(x)的不动点, 则(-x0,-y0)也为f(x)的不动点。 从而n为正奇数………………………………8分
从而 又 \当x=3时,取得最小值,最小值为 |

练习册系列答案
相关题目



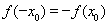











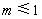
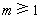
 ,若存在实数
,若存在实数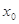 ,使
,使 成立,则称
成立,则称 的不动点.
的不动点. 时,求
时,求 ,函数
,函数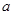 的取值范围;
的取值范围;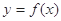 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.