题目内容
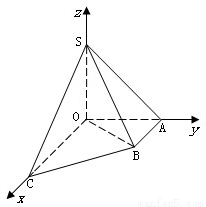
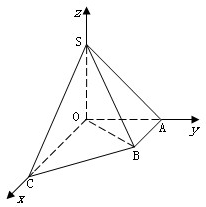
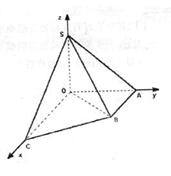
如图直角梯形OABC中,∠COA=∠OAB=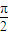 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.(1)求
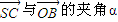 的大小(用反三角函数表示);
的大小(用反三角函数表示);(2)设
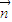 =(1,p,q),满足
=(1,p,q),满足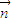 ⊥平面SBC,求:
⊥平面SBC,求:①
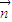 的坐标;
的坐标;②OA与平面SBC的夹角β(用反三角函数表示);
③O到平面SBC的距离.
(3)设
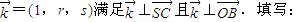
①
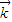 的坐标为______.
的坐标为______.②异面直线SC、OB的距离为______
【答案】分析:(I)根据已知中,∠COA=∠OAB= ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,我们求出各顶点的坐标,进而求出向量
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,我们求出各顶点的坐标,进而求出向量 坐标,代入向量夹角公式,即可得到结论.
坐标,代入向量夹角公式,即可得到结论.
(II)①由已知中得向量 =(1,p,q)为平面SBC的法向量,根据法向量根平面内任一个向量均垂直,数量积均为0,构造方程组,即可求出
=(1,p,q)为平面SBC的法向量,根据法向量根平面内任一个向量均垂直,数量积均为0,构造方程组,即可求出 的坐标;②A与平面SBC的夹角β与OA的方向向量与
的坐标;②A与平面SBC的夹角β与OA的方向向量与 的夹角互余,求出OA的方向向量,代入即可得到结论;
的夹角互余,求出OA的方向向量,代入即可得到结论;
(III)①根据两向量垂直数量积为0,构造关于r,s的方程组,解方程组求出r,s,代入即可求出 的坐标;②由(I)中直线SC、OB的夹角,结合四面体S-OBC的体积,根据V=
的坐标;②由(I)中直线SC、OB的夹角,结合四面体S-OBC的体积,根据V= •d,(其中θ为两条异面直线夹角,d为两条异面直线的夹角),即可得到答案.
•d,(其中θ为两条异面直线夹角,d为两条异面直线的夹角),即可得到答案.
解答:解:(Ⅰ)如图所示:
C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0)
∴
∴ (4分)
(4分)
(Ⅱ)① ∴
∴ ,∴
,∴
 ,∴
,∴ (7分)
(7分)
②过O作OE⊥BC于E,则BC⊥面SOE,∴SOE⊥SAB又两面交于SE,过O作OH⊥SE于H,则OH⊥SBC,延长OA与CB交于F,则OF=2
连FH,则∠OFH为所求
 ,∴
,∴ ∴
∴ ,
,
∴
∴
③由题设条件可得∠OBC是直角,可得出CB⊥面SOB,故CB⊥SB
又在直角三角形SOB内,可求得SB= ,在梯形OABC内,可求得BC=
,在梯形OABC内,可求得BC= ,于是可得
,于是可得
又由题设条件得 =
=
故由等体积法可得点O到面SBC的距离为 =
=
(III) (1,-1,2);
(1,-1,2); (14分).
(14分).
点评:本题考查的知识点是用空间向量求直线与平面的夹角,用空间向量求直线间夹角、距离,其中熟练掌握两个向量垂直,数量积为0,及向量夹角公式是解答本题的关键.
 ,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,我们求出各顶点的坐标,进而求出向量
,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,我们求出各顶点的坐标,进而求出向量 坐标,代入向量夹角公式,即可得到结论.
坐标,代入向量夹角公式,即可得到结论.(II)①由已知中得向量
 =(1,p,q)为平面SBC的法向量,根据法向量根平面内任一个向量均垂直,数量积均为0,构造方程组,即可求出
=(1,p,q)为平面SBC的法向量,根据法向量根平面内任一个向量均垂直,数量积均为0,构造方程组,即可求出 的坐标;②A与平面SBC的夹角β与OA的方向向量与
的坐标;②A与平面SBC的夹角β与OA的方向向量与 的夹角互余,求出OA的方向向量,代入即可得到结论;
的夹角互余,求出OA的方向向量,代入即可得到结论;(III)①根据两向量垂直数量积为0,构造关于r,s的方程组,解方程组求出r,s,代入即可求出
 的坐标;②由(I)中直线SC、OB的夹角,结合四面体S-OBC的体积,根据V=
的坐标;②由(I)中直线SC、OB的夹角,结合四面体S-OBC的体积,根据V= •d,(其中θ为两条异面直线夹角,d为两条异面直线的夹角),即可得到答案.
•d,(其中θ为两条异面直线夹角,d为两条异面直线的夹角),即可得到答案.解答:解:(Ⅰ)如图所示:
C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0)
∴

∴
 (4分)
(4分)(Ⅱ)①
 ∴
∴ ,∴
,∴
 ,∴
,∴ (7分)
(7分)②过O作OE⊥BC于E,则BC⊥面SOE,∴SOE⊥SAB又两面交于SE,过O作OH⊥SE于H,则OH⊥SBC,延长OA与CB交于F,则OF=2
连FH,则∠OFH为所求
 ,∴
,∴ ∴
∴ ,
,∴

∴

③由题设条件可得∠OBC是直角,可得出CB⊥面SOB,故CB⊥SB
又在直角三角形SOB内,可求得SB=
 ,在梯形OABC内,可求得BC=
,在梯形OABC内,可求得BC= ,于是可得
,于是可得
又由题设条件得
 =
=
故由等体积法可得点O到面SBC的距离为
 =
=
(III)
 (1,-1,2);
(1,-1,2); (14分).
(14分).点评:本题考查的知识点是用空间向量求直线与平面的夹角,用空间向量求直线间夹角、距离,其中熟练掌握两个向量垂直,数量积为0,及向量夹角公式是解答本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 如图直角梯形OABC中,∠COA=∠OAB=
如图直角梯形OABC中,∠COA=∠OAB= 如图直角梯形OABC位于平面直角坐标系中,其中OC=1,BC=1,OA=2,动点P从C出发沿折线段CBA运动到A(包括端点),设点P的横坐标为x,函数f(x)=
如图直角梯形OABC位于平面直角坐标系中,其中OC=1,BC=1,OA=2,动点P从C出发沿折线段CBA运动到A(包括端点),设点P的横坐标为x,函数f(x)=
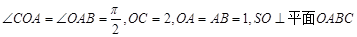 ,
,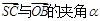 的余弦值;
的余弦值;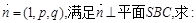
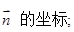
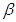 ,求
,求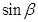 。
。