题目内容
已知数列 满足
满足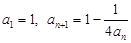 ,其中
,其中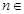 N*.
N*.
(Ⅰ)设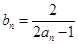 ,求证:数列
,求证:数列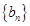 是等差数列,并求出
是等差数列,并求出 的通项公式
的通项公式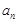 ;
;
(Ⅱ)设 ,数列
,数列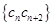 的前
的前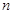 项和为
项和为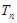 ,是否存在正整数
,是否存在正整数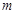 ,使得
,使得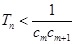 对于
对于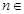 N*恒成立,若存在,求出
N*恒成立,若存在,求出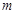 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
(I) .
.
(II)  的最小值为
的最小值为 .
.
解析试题分析:(I)证明 ,
,
所以数列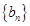 是等差数列,
是等差数列, ,因此
,因此 ,由
,由 得
得 .
.
(II) ,
, ,所以
,所以 ,
,
依题意要使 对于
对于 恒成立,只需
恒成立,只需
解得 或
或 ,所以
,所以 的最小值为
的最小值为 .
.
考点:本题主要考查等差数列的通项公式,“裂项相消法”。
点评:中档题,利用数列的递推公式,进一步确定数列的特征,从而得到等差数列通项公式,数列求和问题中, “错位相减法”、“裂项相消法”、“分组求和法”是高考常常考查到数列求和方法。本题为证明不等式,先求和、再放缩、做结论。

练习册系列答案
相关题目
 、
、 中,
中, ,且当
,且当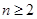 时,
时,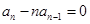 ,
,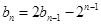 .记
.记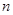 的阶乘
的阶乘 .
.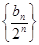 为等差数列;
为等差数列;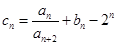 ,求
,求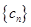 的前
的前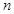 项和.
项和.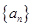 的前n项和为
的前n项和为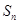 ,且
,且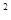 +20n,n∈N
+20n,n∈N .
.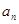 ;
; 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列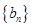 的通项公式及其前n项和
的通项公式及其前n项和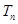 .
.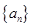 满足:
满足: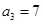 ,
,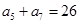 ,
,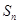 .
.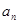 及
及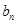 =
=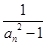 (
(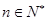 ),求数列
),求数列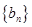 的前
的前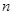 项和
项和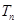 .
. 满足
满足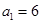 ,
,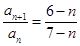
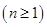 ;
;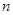 项和
项和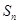 ,并求当
,并求当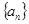 满足:
满足: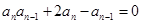 ,
, 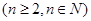 ,
, ,前
,前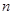 项和为
项和为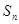 的数列
的数列 满足:
满足: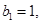
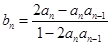
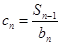
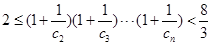
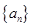 对任意
对任意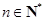 ,满足
,满足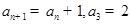 .
.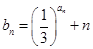 ,求
,求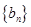 的通项公式及前
的通项公式及前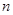 项和.
项和.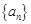 的前
的前 项和为
项和为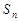 ,若对任意
,若对任意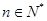 ,都有
,都有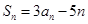 .
.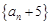 是等比数列,并求数列
是等比数列,并求数列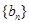 满足
满足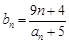 ,问是否存在
,问是否存在 ,使得
,使得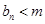 恒成立?如果存在,求出
恒成立?如果存在,求出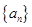 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且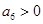 ,
,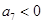 .
. 项和
项和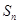 的最大值;
的最大值; 时,求
时,求